题目内容
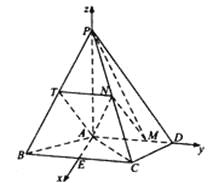
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
【答案】(Ⅰ)详见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)取![]() 的中点
的中点![]() ,然后结合条件中的数据证明四边形
,然后结合条件中的数据证明四边形![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,由此结合线面平行的判定定理可证;(Ⅱ)以
,由此结合线面平行的判定定理可证;(Ⅱ)以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系,然后通过求直线
轴正方向,建立空间直角坐标系,然后通过求直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量的夹角的余弦值来求解
的法向量的夹角的余弦值来求解![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(Ⅰ)由已知得![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,由
,由![]() 为
为![]() 中点知
中点知![]() ,
,![]() .
.
又![]() ,故
,故![]() ,四边形
,四边形![]() 为平行四边形,于是
为平行四边形,于是![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]() .由
.由![]() 得
得![]() ,从而
,从而![]() ,且
,且
![]() .
.
以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .由题意知,
.由题意知,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
, 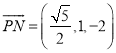 ,
,  .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
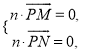 即
即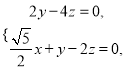
可取![]() .
.
于是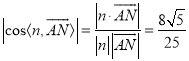 .
.

练习册系列答案
相关题目
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)设该公司从至少消费两次,求这的顾客消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出2人中恰有1人消费两次的概率.



