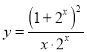题目内容
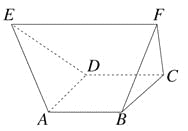
【题目】如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
本题主要考查几何体体积的求法,解题的关键是将不规则的几何体分别分割成规则的几何体.
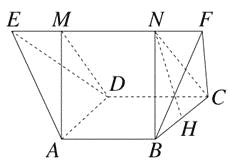
如图,过A,B两点分别作AM,BN垂直于EF,垂足分别为M,N,连接DM,CN,可证得DM⊥EF,CN⊥EF,多面体ABCDEF分为三部分,多面体的体积为VABCDEF=VAMD-BNC+VE-AMD+VF-BNC.
∵NF=![]() ,BF=1,∴BN=
,BF=1,∴BN=![]() .
.
作NH垂直BC于点H,则H为BC的中点,
则NH=![]() .
.
∴S△BNC=![]() ·BC·NH=
·BC·NH=![]() ×1×
×1×![]() =
=![]() .
.
∴VF-BNC=![]() ·S△BNC·NF=
·S△BNC·NF=![]() ,
,
VE-AMD=VF-BNC=![]() ,
,
VAMD-BNC=S△BNC·MN=![]() .
.
∴VABCDEF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目