题目内容
已知椭圆的两个焦点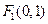 、
、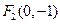 ,直线
,直线 是它的一条准线,
是它的一条准线,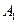 、
、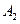 分别是椭圆的上、下两个顶点.
分别是椭圆的上、下两个顶点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设以原点为顶点,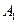 为焦点的抛物线为
为焦点的抛物线为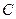 ,若过点
,若过点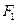 的直线与
的直线与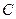 相交于不同
相交于不同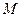 、
、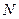 的两点、,求线段
的两点、,求线段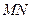 的中点
的中点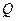 的轨迹方程.
的轨迹方程.
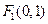 、
、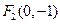 ,直线
,直线 是它的一条准线,
是它的一条准线,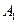 、
、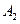 分别是椭圆的上、下两个顶点.
分别是椭圆的上、下两个顶点.(Ⅰ)求椭圆的方程;
(Ⅱ)设以原点为顶点,
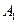 为焦点的抛物线为
为焦点的抛物线为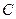 ,若过点
,若过点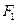 的直线与
的直线与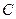 相交于不同
相交于不同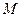 、
、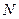 的两点、,求线段
的两点、,求线段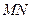 的中点
的中点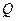 的轨迹方程.
的轨迹方程.(1) (2)
(2)
 (2)
(2)
(Ⅰ)设椭圆方程为==1(a>b>0)
由题意,得c=1,=4 Þ a=2,从而b2=3
∴椭圆的方程 ;
;
(Ⅱ)设抛物线C的方程为x2=2py(p>0)
由=2 Þ p=4
∴抛物线方程为x2=8y
设线段MN的中点Q(x,y),直线l的方程为y=kx+1
由 得
得 ,(这里△≥0恒成立),
,(这里△≥0恒成立),
设M(x1,y1),N(x2,y2)
由韦达定理,得 ,
, ,
,
所以中点坐标为Q ,
,
∴x=4k,y=4k2+1
消去k得Q点轨迹方程为:x2=4(y-1)
由题意,得c=1,=4 Þ a=2,从而b2=3
∴椭圆的方程
 ;
;(Ⅱ)设抛物线C的方程为x2=2py(p>0)
由=2 Þ p=4
∴抛物线方程为x2=8y
设线段MN的中点Q(x,y),直线l的方程为y=kx+1
由
 得
得 ,(这里△≥0恒成立),
,(这里△≥0恒成立),设M(x1,y1),N(x2,y2)
由韦达定理,得
 ,
, ,
,所以中点坐标为Q
 ,
,∴x=4k,y=4k2+1
消去k得Q点轨迹方程为:x2=4(y-1)

练习册系列答案
相关题目
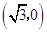 ,一条渐近线m:
,一条渐近线m: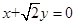 ,设过点A
,设过点A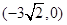 的直线l的方向向量
的直线l的方向向量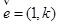 。
。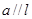 ,且a与l的距离为
,且a与l的距离为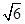 ,求K的值;
,求K的值;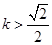 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 中,动点P到两定点
中,动点P到两定点 ,
,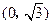 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为 ,过点
,过点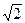 ),对应的准线方程为y=-
),对应的准线方程为y=-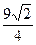 ,且离心率e满足:
,且离心率e满足: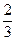 ,e,
,e, 成等比数列.
成等比数列.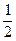
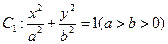 的左、右焦点分别为
的左、右焦点分别为 、
、 ,其中
,其中 的焦点,
的焦点, 是
是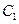 与
与 在第一象限的交点,且
在第一象限的交点,且 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆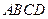 的顶点A﹑C在椭圆
的顶点A﹑C在椭圆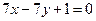 上,求直线
上,求直线 的方程.
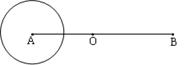
的方程. (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
 与圆
与圆 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
 。
。
 表示斜率为1,在
表示斜率为1,在 轴上的截距为2的直线
轴上的截距为2的直线 三个顶点的坐标是
三个顶点的坐标是 ,中线
,中线 的方程是
的方程是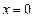
 轴距离为5的点的轨迹方程是
轴距离为5的点的轨迹方程是