题目内容
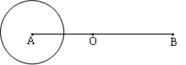
如图所示,O是线段AB的中点,|AB|=2c,以点A为圆心,2a为半径作一圆,其中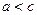 。
。
(1)若圆A外的动点P到B的距离等于它到圆周的最短距离,建立适当坐标系,求动点P的轨迹方程,并说明轨迹是何种曲线;
(2)经过点O的直线l与直线AB成60°角,当c=2,a=1时,动点P的轨迹记为E,设过点B的直线m交曲线E于M、N两点,且点M在直线AB的上方,求点M到直线l的距离d的取值范围。
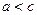 。
。
(1)若圆A外的动点P到B的距离等于它到圆周的最短距离,建立适当坐标系,求动点P的轨迹方程,并说明轨迹是何种曲线;
(2)经过点O的直线l与直线AB成60°角,当c=2,a=1时,动点P的轨迹记为E,设过点B的直线m交曲线E于M、N两点,且点M在直线AB的上方,求点M到直线l的距离d的取值范围。
轨迹方程为: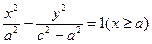 。
。
(2)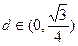
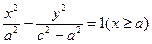 。
。(2)
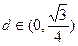
(1)以直线AB为x轴,线段AB的垂直平分线为y轴建立直角坐标系,则A(-c,0),B(c,0)
依题意: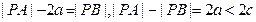
∴点P的轨迹为以A、B为焦点,实半轴为a,虚半轴为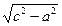 的双曲线右支
的双曲线右支
∴轨迹方程为: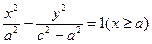 。
。
(2)法一:设M(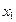 ,
,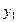 ),N(
),N(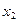 ,
,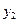 )
)
依题意知曲线E的方程为
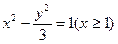 ,l的方程为
,l的方程为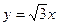
设直线m的方程为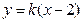
由方程组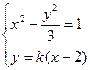 ,消去y得
,消去y得
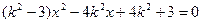 ①
①
∴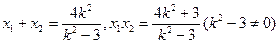
∵直线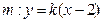 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点
∴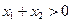 及
及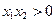 ,从而
,从而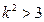
由①得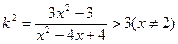
解得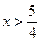 且
且
当x=2时,直线m垂直于x轴,符合条件,∴
又设M到l的距离为d,则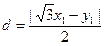
∵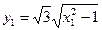
∴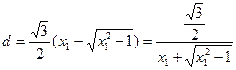
设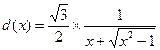 ,
,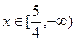
由于函数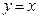 与
与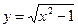 均为区间
均为区间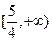 的增函数
的增函数
∴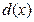 在
在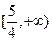 单调递减
单调递减
∴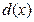 的最大值=
的最大值=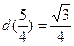
又∵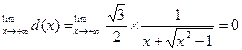
而M的横坐标 ,∴
,∴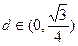
法二: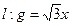 为一条渐近线
为一条渐近线
①m位于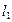 时,m在无穷远,此时
时,m在无穷远,此时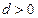
②m位于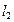 时,
时,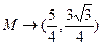 ,d较大
,d较大
由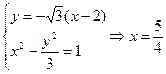
点M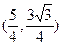
∴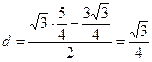
故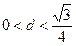
依题意:
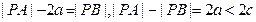
∴点P的轨迹为以A、B为焦点,实半轴为a,虚半轴为
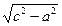 的双曲线右支
的双曲线右支∴轨迹方程为:
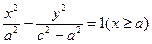 。
。(2)法一:设M(
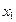 ,
,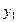 ),N(
),N(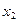 ,
,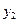 )
)依题意知曲线E的方程为
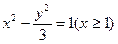 ,l的方程为
,l的方程为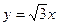
设直线m的方程为
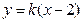
由方程组
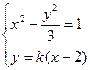 ,消去y得
,消去y得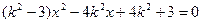 ①
①∴
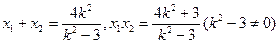
∵直线
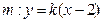 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点∴
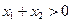 及
及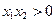 ,从而
,从而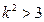
由①得
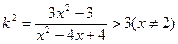
解得
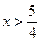 且
且
当x=2时,直线m垂直于x轴,符合条件,∴

又设M到l的距离为d,则
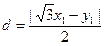
∵
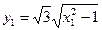
∴
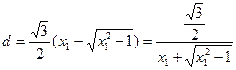
设
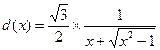 ,
,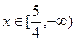
由于函数
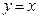 与
与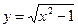 均为区间
均为区间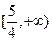 的增函数
的增函数∴
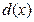 在
在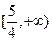 单调递减
单调递减∴
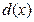 的最大值=
的最大值=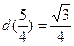
又∵
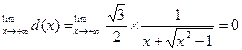
而M的横坐标
 ,∴
,∴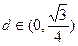
法二:
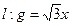 为一条渐近线
为一条渐近线①m位于
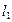 时,m在无穷远,此时
时,m在无穷远,此时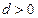
②m位于
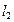 时,
时,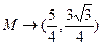 ,d较大
,d较大由
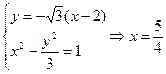
点M
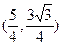
∴
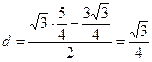
故
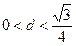

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,动点
,动点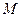 在双曲线
在双曲线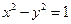 上运动,且
上运动,且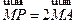 ,求点P的轨迹方程.
,求点P的轨迹方程. 、
、 ,直线
,直线 是它的一条准线,
是它的一条准线, 、
、 分别是椭圆的上、下两个顶点.
分别是椭圆的上、下两个顶点. ,若过点
,若过点 的直线与
的直线与 、
、 的两点、,求线段
的两点、,求线段 的中点
的中点 的轨迹方程.
的轨迹方程.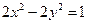 共焦点,且过(
共焦点,且过(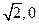 )
)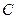 :
: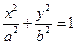
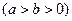 的两个焦点为
的两个焦点为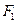 、
、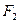 ,点
,点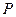 在椭圆
在椭圆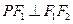 ,
,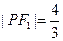 ,
,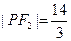 .
. 过圆
过圆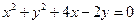 的圆心
的圆心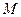 ,交椭圆
,交椭圆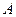 、
、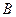 两点,且
两点,且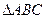 的两个顶点
的两个顶点 的坐标分别为
的坐标分别为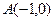 ,
,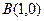 ,平面内两点
,平面内两点 同时满足下列条件:
同时满足下列条件: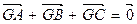 ;②
;②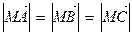 ;③
;③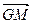 ∥
∥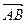
 的轨迹方程;
的轨迹方程;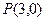 的直线
的直线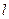 与(1)中轨迹交于
与(1)中轨迹交于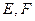 两点,求
两点,求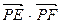 的取值范围
的取值范围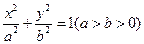 的离心率
的离心率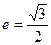 ,过A(a,0),
,过A(a,0),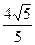 .
. 0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.
0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.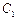 和椭圆
和椭圆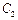 有相同的焦点
有相同的焦点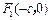 和
和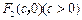 ,两曲线在第一象限内的交点为
,两曲线在第一象限内的交点为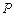 ,椭圆
,椭圆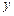 轴负半轴交于点
轴负半轴交于点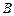 ,且
,且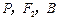 三点共线,
三点共线,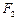 分有向线段
分有向线段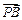 的比为
的比为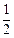 ,又直线
,又直线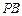 与双曲线
与双曲线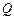 ,若
,若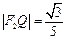 .
.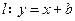 与曲线
与曲线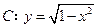 有两个公共点,求实数
有两个公共点,求实数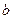 的取值范围.
的取值范围.