题目内容
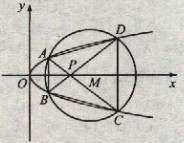
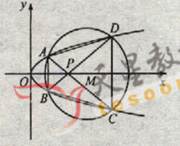 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线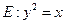
 与圆
与圆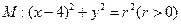 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。(Ⅰ)求r的取值范围
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
(Ⅰ)
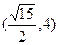 (Ⅱ)(
(Ⅱ)(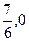 )
)(Ⅰ)联立方程组
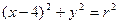 与
与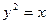 ,可得
,可得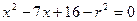 ,所以方程由两个不等式正根
,所以方程由两个不等式正根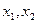
由此得到
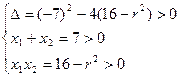 解得
解得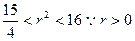 ,所以r的范围为
,所以r的范围为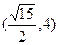
(Ⅱ)不妨设E与M的四个交点坐标分别为设
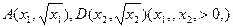
直线AC,BD的方程分别为
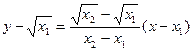 ,
,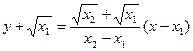
解得点p的坐标为
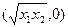 设t=
设t=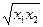 ,由t=
,由t=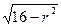 及(1)可知
及(1)可知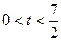
由于四边形ABCD为等腰梯形,因而其面积

将
 代入上式,并令
代入上式,并令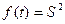 ,得
,得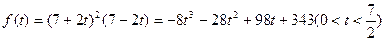
求导数,
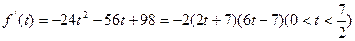
令
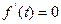 ,解得
,解得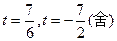
当
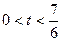 时,
时,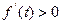 ,当
,当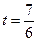 ,
,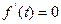 ;当
;当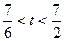 时,
时,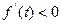
当且仅当
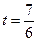 时,
时,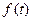 由最大值,即四边形ABCD的面积最大,故所求的点P的坐标为(
由最大值,即四边形ABCD的面积最大,故所求的点P的坐标为(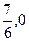 )
)
练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 (
( ),
),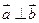 ,动点
,动点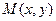 的轨迹为T.
的轨迹为T.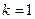 时,已知
时,已知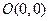 、
、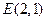 ,试探究是否存在这样的点
,试探究是否存在这样的点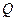 :
: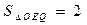 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.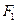 与抛物线
与抛物线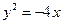 的焦点重合,过
的焦点重合,过 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线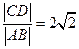 .
. 的最大值和最小值.
的最大值和最小值.
 、
、 ,直线
,直线 是它的一条准线,
是它的一条准线, 、
、 分别是椭圆的上、下两个顶点.
分别是椭圆的上、下两个顶点. ,若过点
,若过点 的直线与
的直线与 、
、 的两点、,求线段
的两点、,求线段 的中点
的中点 的轨迹方程.
的轨迹方程. 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线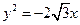 的准线为右准线.
的准线为右准线. :
: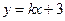 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.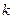 为何值时,使得
为何值时,使得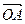
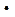
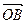
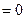 ?
?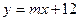 对称?若存在,求出
对称?若存在,求出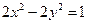 共焦点,且过(
共焦点,且过(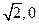 )
) :
: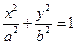
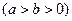 的两个焦点为
的两个焦点为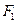 、
、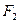 ,点
,点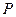 在椭圆
在椭圆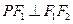 ,
,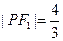 ,
,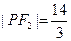 .
. 过圆
过圆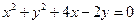 的圆心
的圆心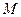 ,交椭圆
,交椭圆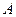 、
、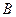 两点,且
两点,且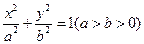 的离心率
的离心率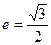 ,过A(a,0),
,过A(a,0),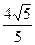 .
. 0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.
0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.

