题目内容
已知数列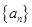 的通项公式为
的通项公式为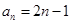 ,数列
,数列 的前
的前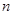 项和为
项和为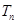 ,且满足
,且满足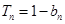 .
.
(1)求 的通项公式;
的通项公式;
(2)在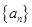 中是否存在使得
中是否存在使得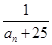 是
是 中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
(1)数列 的通项公式为
的通项公式为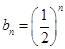 ;(2)存在,如
;(2)存在,如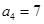 ,
,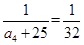 是
是 的第5项.
的第5项.
解析试题分析:(1)首先令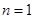 求出
求出 的值,当
的值,当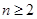 时,
时,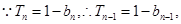 两式相减得:
两式相减得: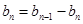 ,即:
,即: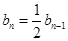 ,从而
,从而 为首项和公比均为
为首项和公比均为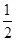 的等比数列,最后利用等比数列的通项公式可求得数列
的等比数列,最后利用等比数列的通项公式可求得数列 的通项公式;(2)先假设存在,即
的通项公式;(2)先假设存在,即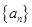 中第
中第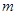 项
项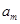 满足题意,亦即
满足题意,亦即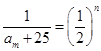 ,故
,故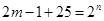 ,因此只要取
,因此只要取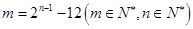 ,就能使得
,就能使得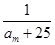 是数列
是数列 中的第
中的第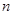 项.
项.
试题解析:(1)当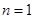 时,
时,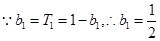 . (2分)
. (2分)
当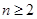 时,
时,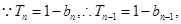 两式相减得:
两式相减得: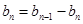 ,即:
,即: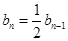 . (6分)
. (6分)
故 为首项和公比均为
为首项和公比均为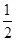 的等比数列,
的等比数列,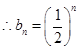 . (8分)
. (8分)
(2)设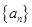 中第
中第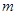 项
项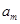 满足题意,即
满足题意,即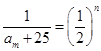 ,即
,即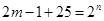 ,所以
,所以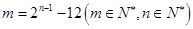 ,取
,取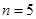 ,则
,则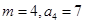 (其它形如
(其它形如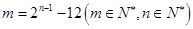 的数均可). (14分)
的数均可). (14分)
考点:1.数列通项公式的求法;2.数列探究型问题的解法.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 ,把
,把 作为新数列
作为新数列 的第一项,把
的第一项,把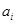 或
或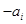 (
(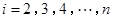 )作为新数列
)作为新数列 项,数列
项,数列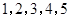 的一个生成数列是
的一个生成数列是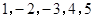 .已知数列
.已知数列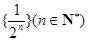 的生成数列,
的生成数列, 为数列
为数列 项和.
项和. 的所有可能值;
的所有可能值;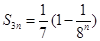 ,求数列
,求数列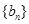 的通项公式;
的通项公式;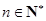 ,
,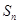 的所有可能值组成的集合为
的所有可能值组成的集合为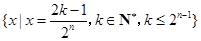 .
.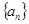 的前
的前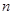 项和为
项和为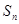 ,且
,且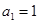 ,
,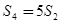 ,数列
,数列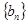 的前
的前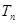 ,满足
,满足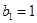 ,
,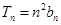 ,
,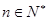 .
. 对所有的
对所有的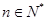 均成立,求实数
均成立,求实数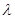 的取值范围.
的取值范围.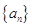 的前
的前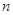 项和为
项和为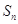 ,
,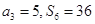 .
. 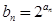 ,求数列
,求数列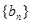 的前
的前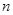 项和
项和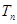 .
.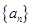 各项为非负实数,前n项和为
各项为非负实数,前n项和为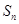 ,且
,且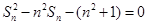
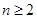 时,求
时,求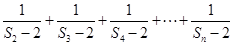 .
.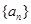 的前
的前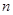 项和为
项和为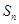 ,已知对任意的
,已知对任意的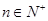 ,点
,点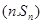 均在函数
均在函数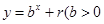 且
且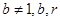 均为常数)的图像上.
均为常数)的图像上.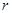 的值;
的值;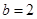 时,记
时,记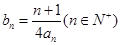 ,求数列
,求数列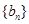 的前
的前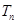 .
.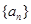 的前
的前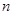 项和为
项和为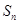 ,且
,且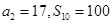 .
.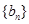 满足
满足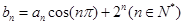 ,求数列
,求数列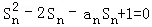 ,n=1,2,3
,n=1,2,3 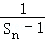 }是等差数列;
}是等差数列;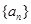 是公比为q的等比数列.
是公比为q的等比数列. 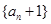 不是等比数列.
不是等比数列.