题目内容
对于数列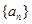 ,把
,把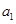 作为新数列
作为新数列 的第一项,把
的第一项,把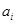 或
或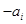 (
(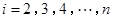 )作为新数列
)作为新数列 的第
的第 项,数列
项,数列 称为数列
称为数列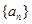 的一个生成数列.例如,数列
的一个生成数列.例如,数列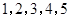 的一个生成数列是
的一个生成数列是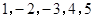 .已知数列
.已知数列 为数列
为数列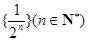 的生成数列,
的生成数列,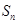 为数列
为数列 的前
的前 项和.
项和.
(1)写出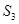 的所有可能值;
的所有可能值;
(2)若生成数列 满足
满足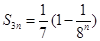 ,求数列
,求数列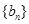 的通项公式;
的通项公式;
(3)证明:对于给定的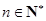 ,
,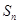 的所有可能值组成的集合为
的所有可能值组成的集合为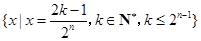 .
.
(1) (2)
(2)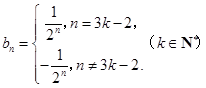 (3)详见解析.
(3)详见解析.
解析试题分析:(1)列举出数列 所有可能情况,共
所有可能情况,共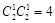 种,分别计算和值为
种,分别计算和值为 ,本题目的初步感观生成数列
,本题目的初步感观生成数列 (2)已知和项解析式,则可利用
(2)已知和项解析式,则可利用 求通项. 当
求通项. 当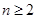 时,
时,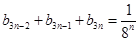 ,而
,而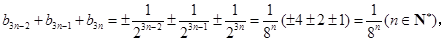 当且仅当
当且仅当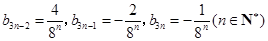 时,才成立.所以
时,才成立.所以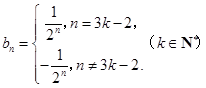 (3)本题实际是对(1)的推广.证明的实质是确定集合
(3)本题实际是对(1)的推广.证明的实质是确定集合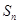 的个数及其表示形式.首先集合
的个数及其表示形式.首先集合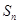 的个数最多有
的个数最多有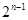 种情形,而每一种的值都不一样,所以个数为
种情形,而每一种的值都不一样,所以个数为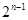 种情形,这是本题的难点,利用同一法证明. 确定集合
种情形,这是本题的难点,利用同一法证明. 确定集合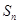 的表示形式,关键在于说明分子为奇数.由
的表示形式,关键在于说明分子为奇数.由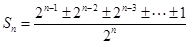 得分子必是奇数,奇数个数由范围
得分子必是奇数,奇数个数由范围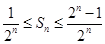 确定.
确定.
试题解析:解:(1)由已知, ,
,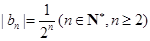 ,
,
∴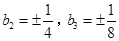 ,
,
由于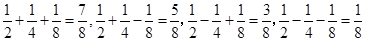 ,
,
∴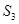 可能值为
可能值为 . 3分
. 3分
(2)∵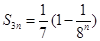 ,
,
当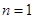 时,
时,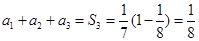 ,
,
当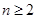 时,
时,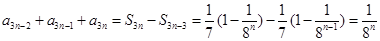 ,
,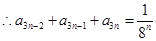 ,
, , 5分
, 5分
∵ 是
是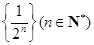 的生成数列,
的生成数列,
∴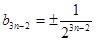 ;
;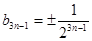 ;
;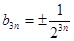 ;
;
∴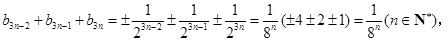
在以上各种组合中,
当且仅当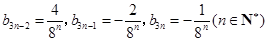 时,才成立.
时,才成立.
∴ . 8分
. 8分
(3)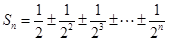 共有
共有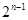 种情形.
种情形.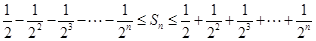 ,即
,即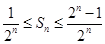 ,
,
又 ,分子必是奇数,
,分子必是奇数,
满足条件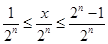 的奇数
的奇数 共有
共有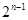 个. 10分
个. 10分
设数列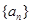 与数列
与数列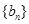 为两个生成数列,数列
为两个生成数列,数列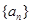 的前
的前 项和为
项和为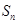 ,数列
,数列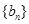 的前
的前 项和为
项和为 ,从第二项开始比较两个数列,设第一个不相等的项为第
,从第二项开始比较两个数列,设第一个不相等的项为第 项.
项.
由于 ,不妨设
,不妨设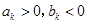 ,
,
则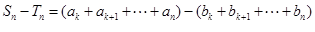
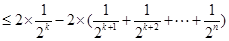
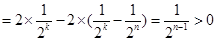

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,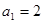 ,对
,对 总有
总有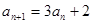 成立,
成立,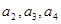 的值;
的值;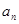 ,并用数学归纳法证明
,并用数学归纳法证明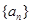 和
和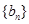 的通项公式分别为
的通项公式分别为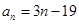 ,
,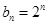 .将
.将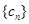 .
.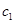 ,
,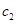 ,
,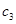 ,
,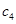 的值,并由此归纳数列
的值,并由此归纳数列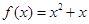 ,用
,用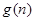 表示
表示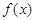 当
当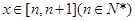 时的函数值中整数值的个数.
时的函数值中整数值的个数.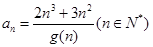 ,求
,求 .
.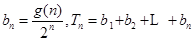 ,若
,若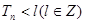 ,求
,求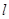 的最小值.
的最小值. 满足:
满足: ,且
,且 ,
,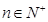 .
.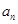 ;
;
 an.
an. 满足:①对任意
满足:①对任意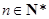 ,
,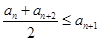 ;②存在常数
;②存在常数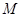 ,对任意
,对任意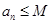 ,则称数列
,则称数列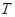 数列”.
数列”.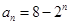
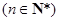 ,证明:数列
,证明:数列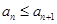 ;
;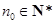 ,数列
,数列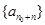 为等差数列.
为等差数列.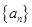 的通项公式为
的通项公式为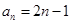 ,数列
,数列 的前
的前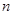 项和为
项和为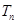 ,且满足
,且满足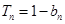 .
.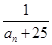 是
是