题目内容
在边长为a的正方形ABCD中,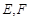 分别为BC,CD的中点,
分别为BC,CD的中点,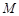 、
、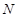 分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥
分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥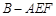 ,如图所示.
,如图所示.
(1)在三棱锥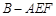 中,求证:
中,求证: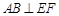 ;
;
(2)求四棱锥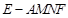 的体积.
的体积.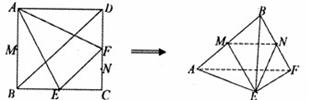
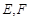 分别为BC,CD的中点,
分别为BC,CD的中点,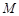 、
、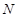 分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥
分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥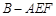 ,如图所示.
,如图所示.(1)在三棱锥
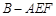 中,求证:
中,求证: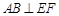 ;
;(2)求四棱锥
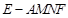 的体积.
的体积.
(1)在三棱锥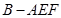 中,因为
中,因为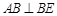 ,
,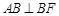 ,
,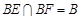 ,
,
所以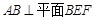 . 又
. 又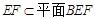 ,所以
,所以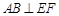 .………………6分
.………………6分
(2)因为在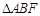 中,
中,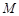 、
、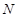 分别为
分别为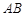 、
、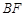 的中点,
的中点,
所以四边形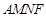 的面积是
的面积是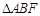 面积的
面积的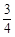 . ………………8分
. ………………8分
又三棱锥 与四棱锥
与四棱锥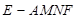 的高相等,
的高相等,
所以,四棱锥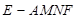 的体积是三棱锥
的体积是三棱锥 的体积的
的体积的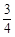 ,
,
因为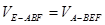 ,所以
,所以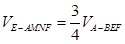 .………………10分
.………………10分
因为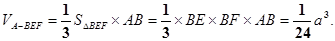
所以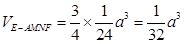 ,故四棱锥
,故四棱锥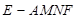 的体积为
的体积为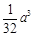 .
.
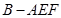 中,因为
中,因为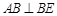 ,
,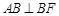 ,
,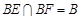 ,
,所以
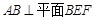 . 又
. 又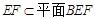 ,所以
,所以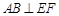 .………………6分
.………………6分(2)因为在
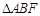 中,
中,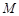 、
、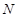 分别为
分别为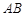 、
、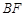 的中点,
的中点,所以四边形
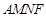 的面积是
的面积是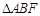 面积的
面积的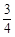 . ………………8分
. ………………8分又三棱锥
 与四棱锥
与四棱锥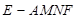 的高相等,
的高相等,所以,四棱锥
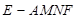 的体积是三棱锥
的体积是三棱锥 的体积的
的体积的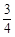 ,
,因为
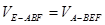 ,所以
,所以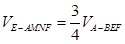 .………………10分
.………………10分因为
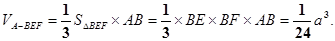
所以
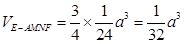 ,故四棱锥
,故四棱锥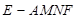 的体积为
的体积为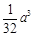 .
.(1)图形的翻折问题,要注意折前折后哪些量发生了变化,哪些量没有变化。
本小题可以证明: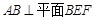 即可.
即可.
(2)求体积可以直接求,也可以通过求其占整个锥体的体积比也可。整个锥体的体积易求。本小题易采用后者。
本小题可以证明:
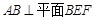 即可.
即可.(2)求体积可以直接求,也可以通过求其占整个锥体的体积比也可。整个锥体的体积易求。本小题易采用后者。

练习册系列答案
相关题目
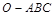 中,
中,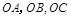 两两垂直且相等,点
两两垂直且相等,点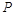 ,
,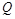 分别是
分别是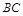 和
和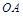 上的动点,且满足
上的动点,且满足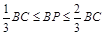 ,
,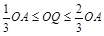 ,则
,则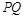 和
和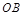 所成角余弦值的取值范围是 .
所成角余弦值的取值范围是 .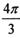 ,则A、B两点的球面距离为________
,则A、B两点的球面距离为________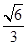 ,求AC的长。
,求AC的长。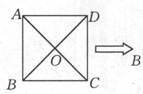
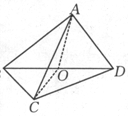
 是长方体
是长方体 被平面
被平面 截去几何体
截去几何体 后得到的几何体,其中
后得到的几何体,其中 为线段
为线段 上异于
上异于 的点,
的点, 为线段
为线段 上异于
上异于 ∥
∥ ,则下列结论中不正确的是
,则下列结论中不正确的是

 表示两个不同的平面,l表示既不在a内也不在
表示两个不同的平面,l表示既不在a内也不在 内的直线,存在以下
内的直线,存在以下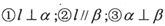 .若以其中两个为条件,另一个为结论,构成命题,
.若以其中两个为条件,另一个为结论,构成命题,
 是
是 的三条高的交点,
的三条高的交点, 平面
平面 ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( ) ②
② ③
③
