题目内容
3.已知某斜三棱柱的三视图如图所示,则该斜三棱柱的表面积为( )
| A. | 4+2$\sqrt{5}$+$\sqrt{6}$ | B. | 4+$\sqrt{5}$+$\sqrt{6}$ | C. | 4+$\sqrt{5}$+2$\sqrt{6}$ | D. | 4+2($\sqrt{5}$+$\sqrt{6}$) |
分析 判断斜三棱柱的底面三角形的形状,棱柱的高,即可求解三棱柱的表面积.
解答 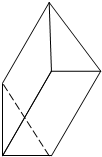 解:由题意可知三棱柱的底面是直角边长为1和2的直角三角形,棱柱的高为:2.
解:由题意可知三棱柱的底面是直角边长为1和2的直角三角形,棱柱的高为:2.
所以该斜三棱柱的表面积为$\frac{1}{2}×1×2×2$+1×2+$\sqrt{{1}^{2}+{2}^{2}}$×1+$\sqrt{6}$=4+$\sqrt{5}$+$\sqrt{6}$.
故选:B.
点评 本题考查三视图求解几何体的表面积,判断几何体的形状是解题的关键…

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.已知$\frac{(1-i)^{2}}{z}$=1+i(i为虚数单位),则复数z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
11.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | y=$\sqrt{1+{x}^{2}}$ | B. | y=x+$\frac{1}{x}$ | C. | y=2x+$\frac{1}{{2}^{x}}$ | D. | y=x+ex |
12.设(1+x)3+(1+x)4+…+(1+x)50=a0+a1x+a2x2+…+a50x50,则a3等于( )
| A. | C${\;}_{51}^{3}$ | B. | C${\;}_{51}^{4}$ | C. | 2C${\;}_{50}^{3}$ | D. | C${\;}_{50}^{4}$ |
13.直线x+my+12=0与直线2x+3y+m=0的交点在y轴上,则m=( )
| A. | -6 | B. | 6 | C. | 24 | D. | ±6 |