题目内容
13.已知函数y=f(x)的定义域为[0,3],则函数y=f(x2-1)的定义域为( )| A. | [0,3] | B. | [-1,8] | C. | [1,2] | D. | [-2,-1]∪[1,2] |
分析 由函数f(x)的定义域为[0,3],知在函数y=f(x2-1)中,0≤x2-1≤3,由此能求出函数y=f(x2-1)的定义域.
解答 解:∵函数f(x)的定义域为[0,3],
∴0≤x≤3
∴在函数y=f(x2-1)中,0≤x2-1≤3,
解得-2≤x≤-1或1≤x≤2,
故函数y=f(x2-1)的定义域为:{[-2,-1]∪[1,2].
故选:D.
点评 本题考查函数的定义域及其解法,是基础题.解题时要认真审题,注意等号.

练习册系列答案
相关题目
6.已知直线l1:ax-y-2=0与直线l2:$\frac{1}{2}$x-y-1=0互相垂直,则实数a的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -2或0 |
4.某工厂为了调查工人文化程度与月收入的关系,随机抽取了部分工人,得到如下列表:
文化程度与月收入列联表(单位:人)
由上表中数据计算得K2=$\frac{{105×{{({10×30-20×45})}^2}}}{55×50×30×75}$≈6.109,请根据下表,估计有多大把握认为“文化程度与月收入有关系”( )
文化程度与月收入列联表(单位:人)
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| A. | 1% | B. | 99% | C. | 2.5% | D. | 97.5% |
18.已知△ABC满足|AB|=3,|AC|=4,O是△ABC所在平面内一点,满足|$\overrightarrow{AO}|=|\overrightarrow{BO}|=|\overrightarrow{CO}$|,且$\overrightarrow{AO}=λ\overrightarrow{AB}+\frac{1-λ}{2}\overrightarrow{AC}$(λ∈R),则cos∠BAC=( )
| A. | $\frac{2}{3}$或$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
5.y=$\frac{{x}^{2}}{x+3}$的导数是( )
| A. | $\frac{{x}^{2}-6x}{(x+3)^{2}}$ | B. | $\frac{{x}^{2}+6x}{x+3}$ | C. | $\frac{{x}^{2}}{(x+3)^{2}}$ | D. | $\frac{{x}^{2}+6x}{(x+3)^{2}}$ |
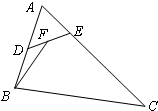 如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )
如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )