Question

1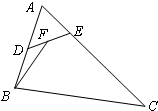．如图，在△ABC中，已知AB=4，AC=6，∠BAC=60°，点D，E分别在边AB，AC上，且$\overrightarrow{AB}$=2$\overrightarrow{AD}$，$\overrightarrow{AC}$=3$\overrightarrow{AE}$，点F为DE中点，则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 可以想着用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{DE}，\overrightarrow{BF}$，并且可以分别表示成：$\overrightarrow{DE}=\frac{1}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$，$\overrightarrow{BF}=\frac{1}{6}\overrightarrow{AC}-\frac{3}{4}\overrightarrow{AB}$，而根据条件可以求出${\overrightarrow{AC}}^{2}，{\overrightarrow{AB}}^{2}，\overrightarrow{AB}•\overrightarrow{AC}$，进行数量积的运算便可得出$\overrightarrow{BF}•\overrightarrow{DE}$的值．

解答 解：由条件：$\overrightarrow{DE}=\overrightarrow{AE}-\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$，$\overrightarrow{BF}=\overrightarrow{DF}-\overrightarrow{DB}=\frac{1}{2}\overrightarrow{DE}-\frac{1}{2}\overrightarrow{AB}$=$\frac{1}{6}\overrightarrow{AC}-\frac{3}{4}\overrightarrow{AB}$；
∴$\overrightarrow{BF}•\overrightarrow{DE}=（\frac{1}{6}\overrightarrow{AC}-\frac{3}{4}\overrightarrow{AB}）$$•（\frac{1}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}）$=$\frac{1}{18}{\overrightarrow{AC}}^{2}-\frac{1}{3}\overrightarrow{AC}•\overrightarrow{AB}+\frac{3}{8}{\overrightarrow{AB}}^{2}$=2-4+6=4．
故选：C．

点评 考查向量减法的几何意义，向量的数乘运算，以及共线向量基本定理，数量积的运算及其计算公式．