题目内容
3.下列两图(图中点与年份对应)分别表示的是某市从2003年到2015年的人均生活用水量和常住人口的情况:
(Ⅰ)若从2003年到2015年中随机选择连续的三年进行观察,求所选的这三年的人均用水量恰好依次递减的概率;
(Ⅱ)由图判断,从哪年开始连续四年的常住人口的方差最大?并结合两幅图表推断该市在2012年到2015年这四年间的总生活用水量的增减情况.(结论不要求证明)
分析 (Ⅰ)挑出满足条件的年份,用古典概率即可求得;
(II)方差表示的就是离散程度,观察即可.
解答 解:(Ⅰ)在13年中共有11个连续的三年…(3分)
其中只有2007至2009和2010至2012两个连续三年的
人均用水量符合依次递减…(6分)
所以随机选择连续的三年进行观察,
所选的这三年的人均用水量恰是依次递减的概率为$\frac{2}{11}$ …(8分)
(Ⅱ)2009至2012连续四年的常住人口的方差最大…(10分)
2012至2015四年间的总生活用水量是递增的.…(12分)
点评 本题考查利用图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
13.已知函数y=f(x)的定义域为[0,3],则函数y=f(x2-1)的定义域为( )
| A. | [0,3] | B. | [-1,8] | C. | [1,2] | D. | [-2,-1]∪[1,2] |
13.sin45°cos15°-cos135°sin165°=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
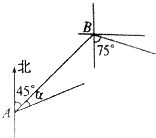 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.