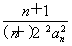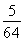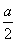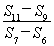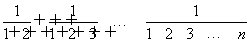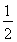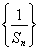题目内容
设无穷数列{an}满足：?n∈Ν?，an<an＋1，an∈N?．记bn＝aan，cn＝aan＋1(n∈N*)．
(1)若bn＝3n(n∈N*)，求证：a1＝2，并求c1的值；
(2)若{cn}是公差为1的等差数列，问{an}是否为等差数列，证明你的结论．
（1）6，证明见解析（2）是
【解析】(1)因为an∈N?，所以若a1＝1，则b1＝aa1＝a1＝3矛盾，
若a1≥3＝aa1，可得1≥a1≥3矛盾，所以a1＝2.于是a2＝aa1＝3，从而c1＝aa1＋1＝a3＝aa2＝6.
(2){an}是公差为1的等差数列，证明如下：an＋1>an?n≥2时，an>an－1，所以an≥an－1＋1?an≥am＋(n－m)，(m<n)
aan＋1＋1≥aan＋1＋an＋1＋1－(an＋1)，即cn＋1－cn≥an＋1－an，由题设，1≥an＋1－an，又an＋1－an≥1，所以an＋1－an＝1，即{an}是等差数列．
练习册系列答案
名校课堂系列答案
相关题目
