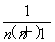题目内容
甲、乙两大超市同时开业,第一年的全年销售额均为a万元,由于经营方式不同,甲超市前n年的总销售额为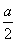 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多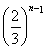 a万元.
a万元.
(1)设甲、乙两超市第n年的销售额分别为an、bn,求an、bn的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?
(1)an=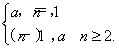 bn=
bn= a(n∈N*)(2)第7年乙超市的年销售额不足甲超市的一半,乙超市将被甲超市收购
a(n∈N*)(2)第7年乙超市的年销售额不足甲超市的一半,乙超市将被甲超市收购
【解析】(1)假设甲超市前n年总销售额为Sn,则Sn=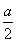 (n2-n+2)(n≥2),因为n=1时,a1=a,则n≥2时,an=Sn-Sn-1=
(n2-n+2)(n≥2),因为n=1时,a1=a,则n≥2时,an=Sn-Sn-1=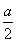 (n2-n+2)-
(n2-n+2)-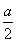 [(n-1)2-(n-1)+2]=a(n-1),故an=
[(n-1)2-(n-1)+2]=a(n-1),故an=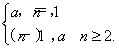 又b1=a,n≥2时,bn-bn-1=
又b1=a,n≥2时,bn-bn-1=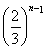 a,故bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=a+
a,故bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=a+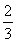 a+
a+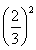 a+…+
a+…+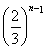 a=
a= a=
a=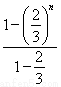 a=
a= a,显然n=1也适合,故bn=
a,显然n=1也适合,故bn= a(n∈N*).
a(n∈N*).
(2)当n=2时,a2=a,b2=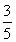 a,有a2>
a,有a2>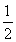 b2;n=3时,a3=2a,b3=
b2;n=3时,a3=2a,b3=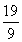 a,有a3>
a,有a3>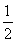 b3;当n≥4时,an≥3a,而bn<3a,故乙超市有可能被甲超市收购.
b3;当n≥4时,an≥3a,而bn<3a,故乙超市有可能被甲超市收购.
当n≥4时,令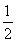 an>bn,则
an>bn,则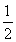 (n-1)a>
(n-1)a> a
a
n-1>6-4·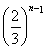 .即n>7-4·
.即n>7-4·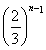 .又当n≥7时,0<4·
.又当n≥7时,0<4·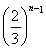 <1,
<1,
故当n∈N*且n≥7时,必有n>7-4·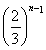 .
.
即第7年乙超市的年销售额不足甲超市的一半,乙超市将被甲超市收购.

练习册系列答案
相关题目