题目内容
各项均为正数的等比数列{an}满足a1a7=4,a6=8,若函数f(x)=a1x+a2x2+a3x3+…+a10x10的导数为f′(x),则f′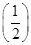 =________.
=________.
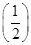 =________.
=________.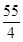
因为各项均为正数的等比数列{an}满足a1a7=4,a6=8,所以a4=2,q=2,故an=2n-3,又f′(x)=a1+2a2x+3a3x2+…+10a10x9,所以f′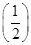 =2-2+2×2-2+3×2-2+…+10×2-2=2-2×
=2-2+2×2-2+3×2-2+…+10×2-2=2-2×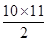 =
=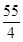 .
.
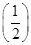 =2-2+2×2-2+3×2-2+…+10×2-2=2-2×
=2-2+2×2-2+3×2-2+…+10×2-2=2-2×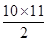 =
=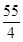 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
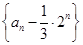 是等比数列;
是等比数列;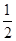 an=1.
an=1.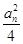 ,数列
,数列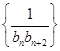 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn<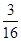 .
.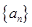 满足
满足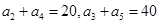 ,则前
,则前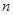 项
项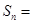 ___ __.
___ __.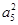 ,a2=1,则a1=________.
,a2=1,则a1=________.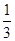
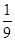
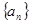 是等比数列,前
是等比数列,前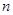 项和为
项和为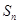 ,
, ,则
,则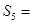
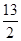

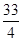
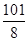
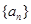 中,
中,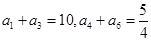 ,则等比数列
,则等比数列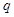 的值为 .
的值为 .