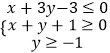题目内容
【题目】已知在直角坐标系xOy中,曲线C1: ![]() (θ为参数),在以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线C2:ρsin(
(θ为参数),在以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线C2:ρsin( ![]() )=1.
)=1.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
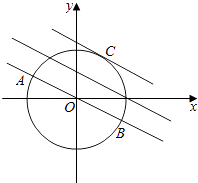
(2)曲线C1上恰好存在三个不同的点到曲线C2的距离相等,分别求这三个点的极坐标.
【答案】
(1)解:曲线C1:  (θ为参数),两式平方相加可得:x2+y2=4,
(θ为参数),两式平方相加可得:x2+y2=4,
曲线C2:ρsin( ![]() )=1,展开可得:
)=1,展开可得: ![]() +
+ ![]() =1,化为直角坐标方程:
=1,化为直角坐标方程: ![]() =0
=0
(2)解:原点O到直线C2: ![]() =0的距离d=
=0的距离d= 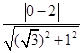 =1=
=1= ![]() r,
r,
直线 ![]() y+x=0与圆的两个交点A,B满足条件.
y+x=0与圆的两个交点A,B满足条件.
联立 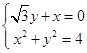 ,解得
,解得 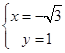 或
或  ,
,
利用 ![]() ,分别化为极坐标A
,分别化为极坐标A ![]() ,B
,B ![]() .
.
设与直线: ![]() =0平行且与圆相切的直线方程为:
=0平行且与圆相切的直线方程为: ![]() y+x+m=0,(m<0).
y+x+m=0,(m<0).
联立 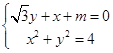 ,化为:4y2+2
,化为:4y2+2 ![]() my+m2﹣4=0,
my+m2﹣4=0,
令△=12m2﹣16(m2﹣4)=0,解得m=﹣4.
∴ ![]() =0,
=0,
解得y= ![]() ,x=1.
,x=1.
∴切点C ![]() ,化为极坐标C
,化为极坐标C ![]() .
.
∴满足条件的这三个点的极坐标分别为:极坐标A ![]() ,B
,B ![]() ,C
,C ![]() .
.
【解析】(1)曲线C1: ![]() (θ为参数),两式平方相加可得直角坐标方程;曲线C2:ρsin(
(θ为参数),两式平方相加可得直角坐标方程;曲线C2:ρsin( ![]() )=1,展开可得:
)=1,展开可得: ![]() +
+ ![]() =1,把
=1,把 ![]() 代入即可化为直角坐标方程.(2)原点O到直线C2:
代入即可化为直角坐标方程.(2)原点O到直线C2: ![]() =0的距离d=1=
=0的距离d=1= ![]() r,直线
r,直线 ![]() y+x=0与圆的两个交点A,B满足条件.联立
y+x=0与圆的两个交点A,B满足条件.联立 ![]() ,解出利用
,解出利用 ![]() ,分别化为极坐标A,B.
,分别化为极坐标A,B.
设与直线: ![]() =0平行且与圆相切的直线方程为:
=0平行且与圆相切的直线方程为: ![]() y+x+m=0,(m<0).与圆的方程联立化为:4y2+2
y+x+m=0,(m<0).与圆的方程联立化为:4y2+2 ![]() my+m2﹣4=0,令△=0,解得m,即可得出.
my+m2﹣4=0,令△=0,解得m,即可得出.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】在某次试验中,有两个试验数据![]() ,统计的结果如下面的表格1.
,统计的结果如下面的表格1.
(1)在给出的坐标系中画出![]() 的散点图; 并判断正负相关;
的散点图; 并判断正负相关;
(2)填写表格2,然后根据表格2的内容和公式求出![]() 对
对![]() 的回归直线方程
的回归直线方程![]() ,并估计当
,并估计当![]() 为10时
为10时![]() 的值是多少?(公式:
的值是多少?(公式: ,
,![]() )
)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 4 | 5 |
表1

表格2
序号 | | | | |
1 | 1 | 2 | ||
2 | 2 | 3 | ||
3 | 3 | 4 | ||
4 | 4 | 4 | ||
5 | 5 | 5 | ||
|
|
|
|