题目内容
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且离心率e为
,且离心率e为 ![]() .
. 
(1)求椭圆E的方程;
(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G ![]() 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
【答案】
(1)解:由已知得 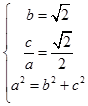 ,解得
,解得 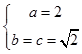 ,
,
∴椭圆E的方程为 ![]()
(2)解:解法一:设点A(x1y1),B(x2,y2),AB中点为H(x0,y0).
由 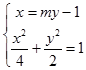 ,化为(m2+2)y2﹣2my﹣3=0,
,化为(m2+2)y2﹣2my﹣3=0,
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,∴y0=
,∴y0= ![]() .
.
G ![]() ,
,
∴|GH|2= ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() .
.
![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故|GH|2﹣ ![]() =
= ![]() +
+ ![]() =
= 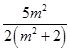 ﹣
﹣ ![]() +
+ ![]() =
= 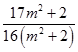 >0.
>0.
∴ ![]() ,故G在以AB为直径的圆外
,故G在以AB为直径的圆外
解法二:设点A(x1y1),B(x2,y2),则 ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
由 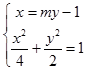 ,化为(m2+2)y2﹣2my﹣3=0,
,化为(m2+2)y2﹣2my﹣3=0,
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,
,
从而 ![]() =
= ![]()
= ![]() +y1y2
+y1y2
= ![]() +
+ ![]()
= 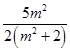 ﹣
﹣ ![]() +
+ ![]() =
= 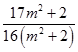 >0.
>0.
∴ ![]() >0,又
>0,又 ![]() ,
, ![]() 不共线,
不共线,
∴∠AGB为锐角.
故点G ![]() 在以AB为直径的圆外
在以AB为直径的圆外
【解析】解法一:(1)由已知得 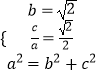 ,解得即可得出椭圆E的方程.(2)设点A(x1,y1),B(x2,y2),AB中点为H(x0,y0).直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,利用根与系数的关系中点坐标公式可得:y0=
,解得即可得出椭圆E的方程.(2)设点A(x1,y1),B(x2,y2),AB中点为H(x0,y0).直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,利用根与系数的关系中点坐标公式可得:y0= ![]() .|GH|2=
.|GH|2= ![]() .
. ![]() =
= ![]() ,作差|GH|2﹣
,作差|GH|2﹣ ![]() 即可判断出.
即可判断出.
解法二:(1)同解法一.(2)设点A(x1,y1),B(x2,y2),则 ![]() =
= ![]() ,
, ![]() =
= ![]() .直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,计算
.直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,计算 ![]() =
= ![]() 即可得出∠AGB,进而判断出位置关系.
即可得出∠AGB,进而判断出位置关系.

练习册系列答案
相关题目
