Question

【题目】已知函数f（x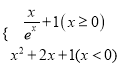）= ，若函数y=f（f（x）﹣a）﹣1有三个零点，则a的取值范围是_____．

Answer 1

【答案】

【解析】当x＜0时，由f（x）﹣1=0得x2+2x+1=1，得x=﹣2或x=0，

当x≥0时，由f（x）﹣1=0得，得x=0，

由，y=f（f（x）﹣a）﹣1=0得f（x）﹣a=0或f（x）﹣a=﹣2，

即f（x）=a，f（x）=a﹣2，

作出函数f（x）的图象如图：

y=≥1（x≥0），

y′=，当x∈（0，1）时，y′＞0，函数是增函数，x∈（1，+∞）时，y′＜0，函数是减函数，

x=1时，函数取得最大值： ，

当1＜a﹣2时，即a∈（3，3+）时，y=f（f（x）﹣a）﹣1有4个零点，

当a﹣2=1+时，即a=3+时则y=f（f（x）﹣a）﹣1有三个零点，

当a＞3+时，y=f（f（x）﹣a）﹣1有1个零点

当a=1+时，则y=f（f（x）﹣a）﹣1有三个零点，

当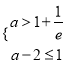时，即a∈（1+，3）时，y=f（f（x）﹣a）﹣1有三个零点．

综上a∈，函数有3个零点．

故答案为： ．