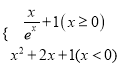题目内容
【题目】设函数f(x)是定义在R上的偶函数，且对任意的x∈R恒有f(x＋1)＝f(x－1)，
已知当x∈[0,1]时f(x)＝(
)1－x，则
①2是函数f(x)的周期；
②函数f(x)在(1,2)上是减函数，在(2,3)上是增函数；
③函数f(x)的最大值是1，最小值是0；
④当x∈(3,4)时，f(x)＝(
)x－3.
其中所有正确命题的序号是_______．
【答案】①②
【解析】由已知条件：f(x＋2)＝f(x)，
则y＝f(x)是以2为周期的周期函数，①正确；
当－1≤x≤0时0≤－x≤1，
f(x)＝f(－x)＝
1＋x，
函数y＝f(x)的图像如图所示：
当3<x<4时，－1<x－4<0，
f(x)＝f(x－4)＝
x－3，因此②④正确，③不正确．
练习册系列答案
相关题目
