题目内容
已知函数f(x)=x|x-a|-lnx,a∈R.
(Ⅰ)若a=1,求函数f(x)在区间[1,e]上的最大值;
(Ⅱ)若f(x)>0恒成立,求a的取值范围.
(1) f(x)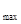 =f(e)=e
=f(e)=e -e-1.
-e-1.
(2) 满足条件的a的取值范围是(-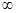 ,1)
,1)
解析试题分析:
考点:解:(Ⅰ)若a=1 ,则f(x)=x|x-1|-lnx.
当x∈[1,e]时,f(x)=x -x-lnx,f′(x)=2x-1-
-x-lnx,f′(x)=2x-1- =
=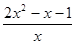 >0,
>0,
所以f(x)在[1,e]上单调递增,∴f(x)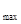 =f(e)=e
=f(e)=e -e-1. 4分
-e-1. 4分
(Ⅱ)函数f(x)的定义域为(0,+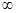 ). 由f(x)>0,得|x-a|>
). 由f(x)>0,得|x-a|>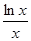 . *
. *
(i)当x∈(0,1)时,|x-a|≥0, 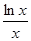 <0,不等式*恒成立,
<0,不等式*恒成立,
所以a∈R; 5分
(ii)当x=1时,|1-a|≥0,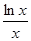 =0,所以a
=0,所以a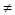 1; 6分
1; 6分
(iii)当x>1时,不等式*恒成立等价于a<x-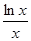 恒成立或a>x+
恒成立或a>x+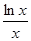 恒成立.
恒成立.
令h(x)=x-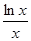 ,则h′(x)=
,则h′(x)=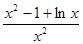 .
.
因为x>1,所以h′(x)>0,从而h(x)>1.
因为a<x-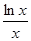 恒成立等价于a<(h(x))
恒成立等价于a<(h(x))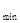 ,所以a≤1.
,所以a≤1.
令g(x)=x+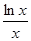 ,则g′(x)=
,则g′(x)=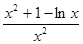 .再令e(x)=x
.再令e(x)=x +1-lnx,则e′(x)=2x-
+1-lnx,则e′(x)=2x- >0在x∈(1,+
>0在x∈(1,+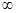 )上恒成立,e(x)在x∈(1,+
)上恒成立,e(x)在x∈(1,+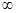 )上无最大值. 11分
)上无最大值. 11分
综上所述,满足条件的a的取值范围是(-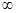 ,1). 12分
,1). 12分
考点:导数的运用
点评:主要是考查了导数在研究函数中的运用,运用导数判定函数单调性以及函数的最值,属于基础题。

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
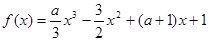 ,其中
,其中 为实数;
为实数; 时,试讨论函数
时,试讨论函数 的零点的个数;
的零点的个数; 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。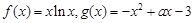 .
.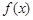 在
在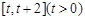 上的最小值;
上的最小值;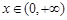 ,
,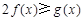 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;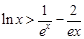 成立.
成立.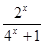 .
. .
. 的单调区间;
的单调区间; 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数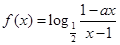 为奇函数,
为奇函数, 为常数.
为常数. 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;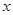 的值,不等式
的值,不等式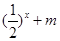 恒成立,求实数
恒成立,求实数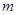 的取值范围.
的取值范围. )的值;
)的值; 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.

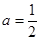 时,求函数
时,求函数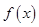 的值域;
的值域;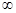 ,+
,+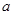 的高考资源网取值范围.
的高考资源网取值范围.