题目内容
已知函数 .
.
(I)求函数 的单调区间;
的单调区间;
(II)若函数 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;
(III)若 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(I) (II)
(II) (III)
(III)
解析试题分析:由已知函数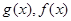 的定义域均为
的定义域均为 ,且
,且 .
.
(Ⅰ)函数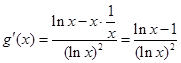 ,
,
当 时,
时,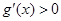 .所以函数
.所以函数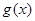 的单调增区间是
的单调增区间是 . 3分
. 3分
(Ⅱ)因f(x)在 上为减函数,故
上为减函数,故 在
在 上恒成立.
上恒成立.
所以当 时,
时,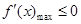 .
.
又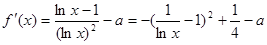 ,
,
故当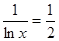 ,即
,即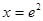 时,
时,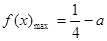 ,所以
,所以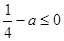 ,故
,故
所以 的最小值为
的最小值为 .
.
(Ⅲ)“若 ,使
,使 成立”等价于
成立”等价于
“当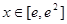 时,有
时,有 ”,
”,
有(Ⅱ),当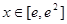 时,有
时,有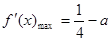 ,
,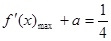 ,
,
问题等价于:“当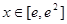 时,有
时,有 ”
”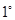 当
当 时,由(Ⅱ),
时,由(Ⅱ), 在
在 上为减函数.
上为减函数.
则 ,故
,故 .
. 当
当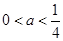 时,由于
时,由于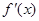
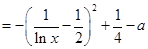 在
在 上为增函数,
上为增函数,
故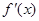 的值域为
的值域为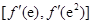 ,即
,即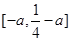 .
.
由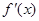 的单调性和值域知,
的单调性和值域知, 唯一
唯一 ,使
,使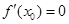 ,且满足:
,且满足:
当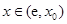 时,
时,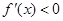 ,
, 为减函数;
为减函数;
当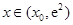 时,
时, ,
, 为增函数;
为增函数;
所以,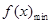 =
=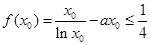 ,
, .
.
所以,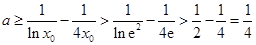 ,与
,与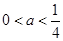 矛盾,不合题意.
矛盾,不合题意.
综上, .
.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查恒成立问题,同时考查不等式的证明,解题的关键是正确求导数,确定函数的单调性.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,其中
,其中 为常数,设
为常数,设 为自然对数的底数.
为自然对数的底数. 时,求
时,求 的最大值;
的最大值; 上的最大值为
上的最大值为 ,求
,求 .
. 的零点;
的零点; 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.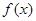 是定义在区间
是定义在区间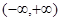 上的偶函数,且满足
上的偶函数,且满足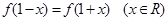
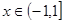 时,
时,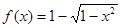 .求使方程
.求使方程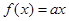 在
在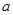 的取值集合M.
的取值集合M.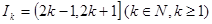 ,
,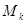 表示使方程
表示使方程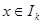 上有两个不相等实根的
上有两个不相等实根的
 时,求
时,求 的解集
的解集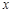 的不等式
的不等式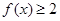 的解集是
的解集是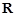 ,求
,求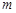 的取值范围
的取值范围
 x;
x; 存在两个零点,求a的取值范围
存在两个零点,求a的取值范围
 都在区间
都在区间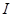 上有定义,对任意
上有定义,对任意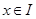 ,都有
,都有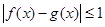 成立,则称函数
成立,则称函数 为区间
为区间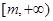 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。 是否为区间
是否为区间 上的“伙伴函数”?
上的“伙伴函数”?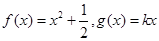 为区间
为区间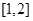 上的“伙伴函数”,求
上的“伙伴函数”,求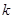 的取值范围
的取值范围 的定义域为
的定义域为 ,
,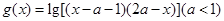 的定义域为
的定义域为 .
.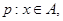
 ,若
,若 是
是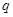 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。