题目内容
定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f (x)=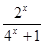 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)证明f (x)在(—1, 0)上时减函数;
(3)当λ取何值时, 不等式f (x)>λ在R上有解?
(1) f(x)=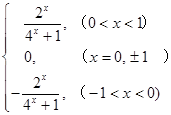 . (2)用定义或导数法均可证明;(3)λ<
. (2)用定义或导数法均可证明;(3)λ<
解析试题分析:(1)当x∈(-1, 0)时, - x∈(0, 1).∴由题意可得f(-x)=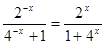 .
.
又f(x)是奇函数,∴f(x)=" -" f (-x) =-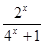 . 2分
. 2分
∵f(-0)= -f(0), ∴f(0)=" 0." 3分
又f(x)是最小正周期为2的函数,∴对任意的x有f(x+2)= f(x).
∴f(-1)=" f(-1+2)=" f(1). 另一面f(-1)="-" f (1), ∴- f(1)=" f(1)" . ∴f(1) = f(-1)=0. 5分
∴f(x)在[-1, 1]上的解析式为 f(x)=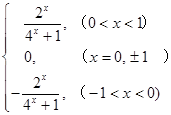 . 6分
. 6分
(2)f (x)在(—1, 0)上时的解析式为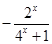 ,∵
,∵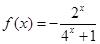 ,∴
,∴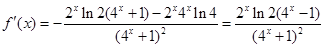 ,又-1<x<0,∴
,又-1<x<0,∴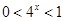 ,∴
,∴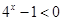 ,∴
,∴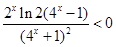 ,∴f (x)在(—1, 0)上时减函数 10分
,∴f (x)在(—1, 0)上时减函数 10分
(3)不等式f(x)>λ在R上有解的λ的取值范围就是λ小于f(x)在R上的最大值.…12分
由(2)结论可得,当x∈(-1, 0)时,有-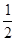 < f(x)= -
< f(x)= -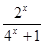 < -
< -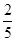 ;
;
又f(x)是奇函数,当x∈(0, 1)时,有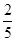 < f(x)=
< f(x)=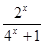 <
<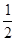 ;
;
∴f(x)在[-1, 1]上的值域是(-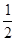 , -
, -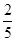 )∪{0}∪(
)∪{0}∪(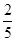 ,
, 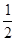 ). 14分
). 14分
由f(x)的周期是2;故f(x)在R上的值域是(-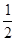 , -
, -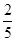 )∪{0}∪(
)∪{0}∪(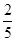 ,
, 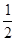 ) 15分
) 15分
∴λ< 时,不等式f(x)>λ在R上有解. 16分
时,不等式f(x)>λ在R上有解. 16分
考点:本题考查了函数的性质
点评:利用奇偶性求函数解析式问题要注意:(1)在哪个区间求解析式,就设在哪个区间里;(2)转化为已知的解析式进行代入;(3)利用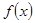 的奇偶性把
的奇偶性把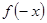 写成
写成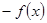 或
或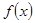 ,从而求出
,从而求出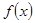 .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案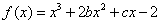 的图象在与
的图象在与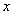 轴交点处的切线方程是
轴交点处的切线方程是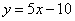 .
. 的解析式;
的解析式;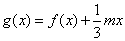 ,若
,若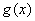 的极值存在,求实数
的极值存在,求实数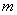 的取值范围以及当
的取值范围以及当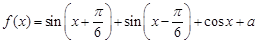 的最大值为1.
的最大值为1.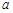 的值;(2)求使
的值;(2)求使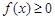 成立的x的取值集合.
成立的x的取值集合.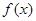 是定义在区间
是定义在区间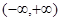 上的偶函数,且满足
上的偶函数,且满足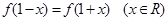
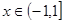 时,
时,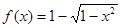 .求使方程
.求使方程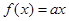 在
在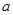 的取值集合M.
的取值集合M.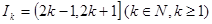 ,
,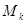 表示使方程
表示使方程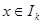 上有两个不相等实根的
上有两个不相等实根的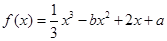 ,
,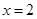 是
是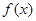 的一个极值点.
的一个极值点.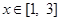 时,
时,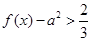 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.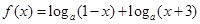 ,其中
,其中 ,记函数
,记函数 的定义域为D.
的定义域为D. ,求
,求 的值;
的值;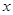 ,不等式
,不等式 <
<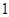 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.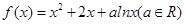 .
.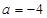 时,求
时,求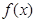 的最小值;
的最小值;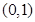 上为单调函数,求实数
上为单调函数,求实数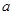 的取值范围;
的取值范围;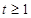 时,不等式
时,不等式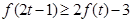 恒成立,求实数
恒成立,求实数