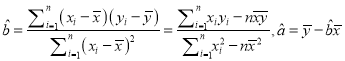Question

【题目】已知数列{an}，a1=1，且an﹣1﹣an﹣1an﹣an=0（n≥2，n∈N*），记bn=a2n﹣1a2n+1 ， 数列{bn}的前n项和为Tn ， 则满足不等式Tn＜ 成立的最大正整数n为 ．

Answer 1

【答案】7
【解析】解：∵an﹣1﹣an﹣1an﹣an=0，
∴ ﹣ =1，
∵a1=1，
∴ =1，
∴数列{ }是以1为首项，1为公差的等差数列，
∴ =1+n﹣1=n，
即an= ，
当n=1是成立，
∴bn=a2n﹣1a2n+1= = （ ﹣ ），
∴Tn=b1+b2+…+bn= （1﹣ + ﹣ +…+ ﹣ ）= （1﹣ ）= ，
∵Tn＜ ，
∴ （1﹣ ）＜ ，
∴2n+1＜17，
即n＜8，
∴满足不等式Tn＜ 成立的最大正整数n为7，
所以答案是：7．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系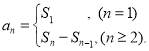才能正确解答此题．