题目内容
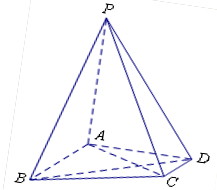
在四棱锥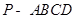 中,
中,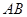 //
//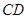 ,
,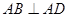 ,
,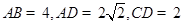 ,
,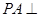 平面
平面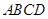 ,
,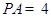 .
.
(1)求证: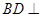 平面
平面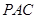 ;
;
(2)求异面直线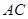 与
与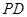 所成角的余弦值;
所成角的余弦值;
(3)设点 为线段
为线段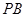 上一点,且直线
上一点,且直线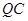 与平面
与平面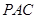 所成角的正弦值为
所成角的正弦值为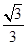 ,求
,求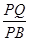 的值.
的值.
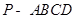 中,
中,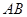 //
//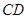 ,
,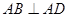 ,
,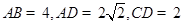 ,
,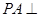 平面
平面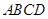 ,
,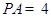 .
. 
(1)求证:
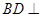 平面
平面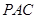 ;
;(2)求异面直线
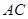 与
与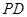 所成角的余弦值;
所成角的余弦值;(3)设点
 为线段
为线段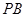 上一点,且直线
上一点,且直线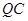 与平面
与平面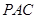 所成角的正弦值为
所成角的正弦值为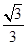 ,求
,求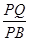 的值.
的值.(1)见解析(2)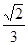 ,(3)
,(3)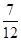
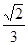 ,(3)
,(3)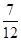
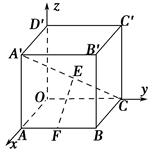
试题分析:(1)建立如图所示坐标系,
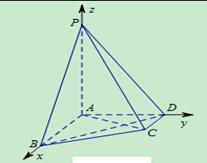
写出
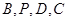 坐标,可得
坐标,可得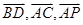 坐标,由
坐标,由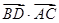 =
= ,
,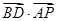 =
= 知
知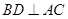 ,
,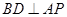 .所以
.所以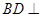 平面
平面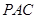 ;(2)由
;(2)由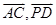 向量的夹角可知异成直线
向量的夹角可知异成直线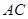 与
与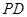 所成角;(3)
所成角;(3) 为线段
为线段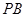 上一点,设
上一点,设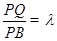 其中
其中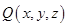 可得
可得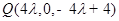 ,由直线
,由直线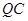 与平面
与平面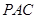 所成角的正弦值为
所成角的正弦值为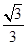 ,利用
,利用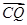 与平面
与平面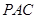 的法向量
的法向量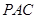 夹角,可得
夹角,可得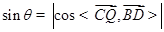 .其中
.其中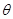 为直线
为直线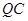 与平面
与平面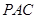 所成角.
所成角.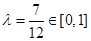 .即
.即 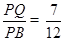 .
.试题解析:(1)证明:
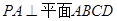 因为,
因为,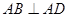 ,所以以
,所以以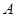 为坐标原点,
为坐标原点,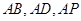 所在的直线分别为
所在的直线分别为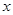 轴、
轴、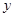 轴、
轴、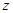 轴建立空间直角坐标系, 1分
轴建立空间直角坐标系, 1分则
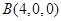 ,
,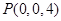 ,
,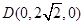 ,
,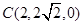 .
.所以
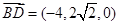 ,
,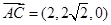 ,
,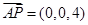 , 2分
, 2分所以
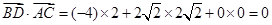 ,
,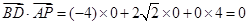 .
.所以
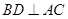 ,
,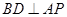 .
. 因为
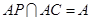 ,
,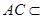 平面
平面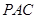 ,
,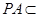 平面
平面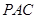 ,
,所以
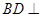 平面
平面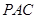 . 4分
. 4分(2)
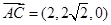 ,
,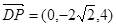 5分
5分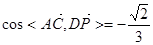
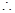 异成直线
异成直线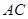 与
与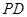 所成角的余弦值
所成角的余弦值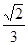 8分
8分(3)解:设
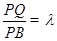 (其中
(其中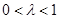 ),
),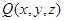 ,直线
,直线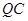 与平面
与平面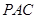 所成角为
所成角为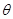 .
.所以
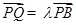 .所以
.所以 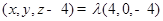 .
.所以
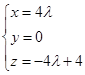 即
即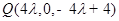 . 9分
. 9分所以
 .
.平面
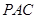 的一个法向量为
的一个法向量为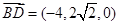 . 10分
. 10分因为
 ,
,所以
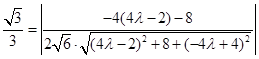 . 11分
. 11分解得
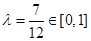 .所以
.所以 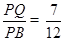 . 12分
. 12分
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
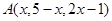
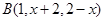 ,当
,当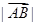 取最小值时,
取最小值时,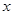 的值等于( )
的值等于( )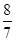
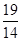
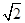 a
a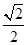 a
a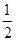 a
a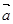 、
、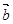 的坐标满足
的坐标满足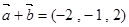 ,
,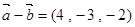 ,则
,则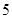
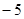
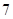
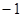
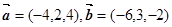
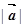 ;(2)求
;(2)求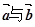 夹角的余弦值.
夹角的余弦值.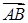 =(2,4,5),
=(2,4,5),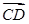 =(3,x,y),若
=(3,x,y),若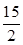
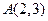 ,
,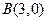 ,且
,且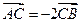 ,则点
,则点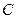 的坐标为 ( )
的坐标为 ( )