题目内容
5.已知AD为△ABC的中线,G为重心,点A为(6,-2),点G为(4,0),则点D的坐标为(3,1).分析 设B点坐标为(a,b),C点坐标为(c,d),根据重心坐标公式,可得a+c=6,b+d=2,再由中点坐标公式,可得答案.
解答 解:设B点坐标为(a,b),C点坐标为(c,d),
∵点A为(6,-2),点G为(4,0),
∴$\frac{1}{3}$(a+c+6)=4,$\frac{1}{3}$(b+d-2)=0,
解得:a+c=6,b+d=2,
∵AD为△ABC的中线,
∴D为BC的中点,
故D的坐标为:(3,1),
故答案为:(3,1)
点评 本题考查中点坐标公式的应用,考查三角形重心坐标公式的应用,难度不大,属于基础题.

练习册系列答案
相关题目
13.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D.则四面体ABCD的四个顶点所在球的半径为( )
| A. | $\frac{5}{2}$ | B. | $\frac{25}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{25}$ |
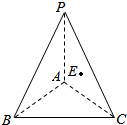 已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,求证:PA⊥平面ABC.
已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,求证:PA⊥平面ABC.