题目内容
17.函数φ(x)=$\frac{1-2{x}^{2}}{1+{x}^{2}}$(x∈R)的值域为(-2,1].分析 将原函数变成φ(x)=$-2+\frac{3}{1+{x}^{2}}$,从而由1+x2≥1,可得出$\frac{1}{1+{x}^{2}}$的范围,从而求出y的范围,即求出原函数的值域.
解答 解:φ(x)=$\frac{1-2{x}^{2}}{1+{x}^{2}}=\frac{-2(1+{x}^{2})+3}{1+{x}^{2}}=-2+\frac{3}{1+{x}^{2}}$;
1+x2≥1;
∴$0<\frac{1}{1+{x}^{2}}≤1$;
∴-2<y≤1;
∴原函数的值域为(-2,1].
故答案为:(-2,1].
点评 考查函数值域的概念,分离常数求函数值域的方法,二次函数的值域,不等式的性质:同向的不等式,取倒数后改变方向.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
9.已知函数f(2-x)=$\sqrt{4x-{x}^{2}}$,则函数f($\sqrt{x}$)的定义域为( )
| A. | [0,+∞) | B. | [0,16] | C. | [0,4] | D. | [0,2] |
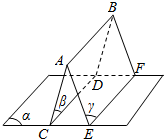 已知α,β,γ为平面,α∩β=CD,α∩γ=EF,β∩γ=AB,AB∥CD,AB?α.求证:
已知α,β,γ为平面,α∩β=CD,α∩γ=EF,β∩γ=AB,AB∥CD,AB?α.求证: