题目内容
8.f(x)=$\left\{\begin{array}{l}\;lgx\;\;\;x>0\\ \;-\frac{1}{x}\;\;\;x<0\end{array}$,则f(x)+x=0的根的个数为( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 f(x)+x=0的根的个数可化为f(x)与y=-x的图象的交点的个数,作函数f(x)=$\left\{\begin{array}{l}\;lgx\;\;\;x>0\\ \;-\frac{1}{x}\;\;\;x<0\end{array}$与函数y=-x的图象,结合图象求解即可.
解答 解:f(x)+x=0的根的个数可化为f(x)与y=-x的图象的交点的个数,
作函数f(x)=$\left\{\begin{array}{l}\;lgx\;\;\;x>0\\ \;-\frac{1}{x}\;\;\;x<0\end{array}$与函数y=-x的图象如下,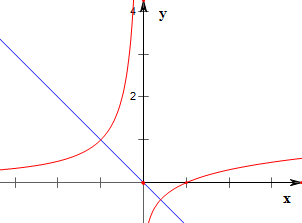
结合图象可得,
f(x)+x=0的根的个数为2个;
故选C.
点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
3.如图所示的程序框图,若输出结果是990,则判断框内应填入的条件是( )


| A. | i≥10 | B. | i<10 | C. | i≥9 | D. | i<9 |
20.已知平面上三点A、B、C满足|AB|=3,|BC|=4,|CA|=5,则$\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{BC}•\overrightarrow{CA}$+$\overrightarrow{CA}•\overrightarrow{AB}$值等于( )
| A. | -25 | B. | -20 | C. | 25 | D. | -10 |
17.设f0(x)=cosx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x)(n∈N),则f2015(x)=( )
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
18.一船向正北方向航行,看见它的正西方向有相距10海里的两个灯塔恰好与它在一条直线上.船继续航行半小时后,看见这两个灯塔恰好与它在一条直线上.船继续航行半个小时后,看见这两个灯塔中,一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是每小时( )
| A. | 5$\sqrt{2}$海里 | B. | 5 海里 | C. | 10$\sqrt{2}$海里 | D. | 10海里 |