题目内容
16.直线kx-y+k=0与圆x2+y2-2x=0有公共点,则实数k的取值范围是( )| A. | $[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$ | B. | $(-∞,-\frac{{\sqrt{3}}}{3}]∪[\frac{{\sqrt{3}}}{3},+∞)$ | C. | $[-\sqrt{3},\sqrt{3}]$ | D. | $(-∞,-\sqrt{3}]∪[\sqrt{3},+∞)$ |
分析 由题意利用点到直线的距离小于等于半径,求出k的范围即可.
解答 解:由题意可知圆的圆心坐标为(1,0),半径为1,
因为直线kx-y+k=0与圆x2+y2-2x=0有公共点,所以$\frac{|2k|}{\sqrt{{k}^{2}+1}}$≤1,
解得-$\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$.
故选:A.
点评 本题是中档题,考查直线与圆的位置关系,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
4.式子$\frac{lo{g}_{8}27}{lo{g}_{2}3}$的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 2 |
8.幂函数f(x)的图象过点$({3,\root{3}{9}})$,则f(8)=( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
6.圆x2+y2-2x-5=0与圆x2+y2+2x-4y-4=0的交点为A,B,则线段AB的垂直平分线的方程是( )
| A. | x+y-1=0 | B. | 2x-y+1=0 | C. | x-2y+1=0 | D. | x-y+1=0 |
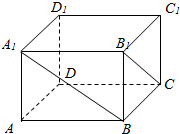 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.