题目内容
7.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=-\frac{\sqrt{2}}{2}t+2}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),以原点O为极点,x轴张半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ.(Ⅰ)若a=2,求圆C的直角坐标方程与直线l的普通方程;
(Ⅱ)设直线l截圆C的弦长等于圆C的半径长的$\sqrt{2}$倍,求a的值.
分析 (Ⅰ)消去参数t可得直线l的普通方程为x+y-2=0,圆C的极坐标方程为ρ2=aρsinθ,即x2+y2=ay,把a=2代入可得;
(Ⅱ)易得圆的圆心为(0,$\frac{a}{2}$),半径为$\frac{|a|}{2}$,可得圆心到直线的距离d,由圆的弦长和半径以及d的关系可得a的方程,解方程可得.
解答 解:(Ⅰ)消去参数t可得直线l的普通方程为x+y-2=0,
∵圆C的极坐标方程为ρ=2sinθ,即ρ2=aρsinθ,∴x2+y2=ay,
当a=2时,可得圆C的直角坐标方程为x2+y2=2y,
化为标准方程可得x2+(y-1)2=1;
(Ⅱ)由(Ⅰ)可得圆C的直角坐标方程为x2+(y-$\frac{a}{2}$)2=$\frac{{a}^{2}}{4}$,
∴圆心为(0,$\frac{a}{2}$),半径为$\frac{|a|}{2}$,
∴圆心到直线l:x+y-2=0的距离d=$\frac{|\frac{a}{2}-2|}{\sqrt{2}}$,
∵直线l截圆C的弦长等于圆C的半径长的$\sqrt{2}$倍,
∴($\frac{|a|}{2}$)2=($\frac{|\frac{a}{2}-2|}{\sqrt{2}}$)2+($\frac{\sqrt{2}a}{4}$)2,
解得a=2.
点评 本题考查参数方程和极坐标方程,涉及直线和圆的位置关系,属中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
7.已知函数y=f(x)=$\left\{\begin{array}{l}{5x,0<x≤13}\\{7x+2,x>13}\end{array}\right.$的定义域是( )
| A. | (0.+∞) | B. | (-∞,0]∪[0,+∞) | C. | (-∞,0]∪(0,+∞) | D. | [0,+∞) |
19.已知f(x)=ax4+bx2-x+m,f(2)=1,则f(-2)=( )
| A. | 5 | B. | 0 | C. | 3 | D. | -2 |
16.直线kx-y+k=0与圆x2+y2-2x=0有公共点,则实数k的取值范围是( )
| A. | $[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$ | B. | $(-∞,-\frac{{\sqrt{3}}}{3}]∪[\frac{{\sqrt{3}}}{3},+∞)$ | C. | $[-\sqrt{3},\sqrt{3}]$ | D. | $(-∞,-\sqrt{3}]∪[\sqrt{3},+∞)$ |
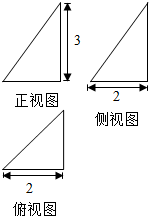 一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.
一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.