题目内容
5.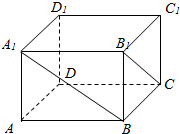 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.(1)求BD1与平面ABCD所成的角的余弦;
(2)求异面直线A1B与B1C所成角的余弦值.
分析 (1)连接BD1,BD,由DD1⊥平面ABCD,得到∠DBD1即BD1与平面ABCD所成的角,分别利用勾股定理求出BD与BD1的长,即可求出BD1与平面ABCD所成的角的余弦;
(2)连接A1D,由A1D∥B1C,得到∠BA1D为异面直线A1B与B1C所成的角,在△A1DB中,利用余弦定理求出cosBA1D的值即可.
解答  解:(1)连接BD1,BD,
解:(1)连接BD1,BD,
∵DD1⊥平面ABCD,
∴∠DBD1即BD1与平面ABCD所成的角,
∵在Rt△ABD中,AD=AB=4,
∴根据勾股定理得:BD=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵在Rt△BDD1中,DD1=3,
∴根据勾股定理得:BD1=$\sqrt{(4\sqrt{2})^{2}+{3}^{2}}$=$\sqrt{41}$,
则cos∠DBD1=$\frac{D{D}_{1}}{BD}$=$\frac{4\sqrt{2}}{\sqrt{41}}$=$\frac{4\sqrt{82}}{41}$;
(2)连接A1D,
∵A1D∥B1C,
∴∠BA1D为异面直线A1B与B1C所成的角,
在△A1DB中,A1B=A1D=5,BD=4$\sqrt{2}$,
则cos∠BA1D=$\frac{{A}_{1}{B}^{2}+{A}_{1}{D}^{2}-B{D}^{2}}{2{A}_{1}B•{A}_{1}D}$=$\frac{25+25-32}{50}$=$\frac{9}{25}$.
点评 此题考查了直线与平面所成的角,异面直线及其所成的角,找出直线与平面所成的角、异面直线所成的角是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.直线kx-y+k=0与圆x2+y2-2x=0有公共点,则实数k的取值范围是( )
| A. | $[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$ | B. | $(-∞,-\frac{{\sqrt{3}}}{3}]∪[\frac{{\sqrt{3}}}{3},+∞)$ | C. | $[-\sqrt{3},\sqrt{3}]$ | D. | $(-∞,-\sqrt{3}]∪[\sqrt{3},+∞)$ |
14.对于函数y=g(x),部分x与y的对应关系如下表:
数列{xn}满足:x1=2,且对于任意n∈N*,点(xn,xn+1)都在函数y=g(x)的图象上,则x1+x2+…+x2015=( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 2 | 4 | 7 | 5 | 1 | 8 |
| A. | 4054 | B. | 5046 | C. | 5075 | D. | 6047 |
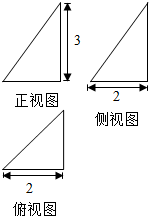 一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.
一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.