题目内容
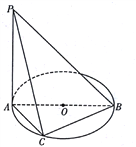
【题目】如图, ![]() 是
是![]() 直径,
直径, ![]() 所在的平面,
所在的平面, ![]() 是圆周上不同于
是圆周上不同于![]() 的动点.
的动点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且当二面角
,且当二面角![]() 的正切值为
的正切值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)先根据圆的性质得![]() ,再根据线面垂直得
,再根据线面垂直得![]() ,根据线面垂直判定定理得
,根据线面垂直判定定理得![]() 平面
平面![]() ,最后根据面面垂直判定定理得结论(2)先根据二面角定义得二面角
,最后根据面面垂直判定定理得结论(2)先根据二面角定义得二面角![]() 的平面角为
的平面角为![]() ,再过过
,再过过![]() 作
作![]() 于
于![]() ,易得
,易得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.最后通过解三角形可得结论
所成的角.最后通过解三角形可得结论
试题解析:(1)证明:∵![]() 在圆
在圆![]() 上,
上, ![]() 为圆
为圆![]() 的直径,
的直径,
∴![]() ,
,
又∵![]() 所在的平面,∴
所在的平面,∴![]() ,
,
而![]() ,∴
,∴![]() 平面
平面![]() ,
,
由于![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:如图,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
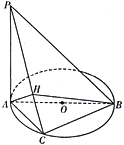
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() ,则
,则![]() 即为所求的角,
即为所求的角,
∵![]() 平面
平面![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
又![]() ,
, ![]() ,∴
,∴![]() ,
,
在![]() 中,
中, 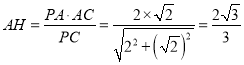 ,
,
在![]() 中,
中, 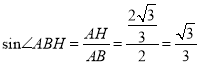 ,
,
即直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() x+
x+![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?



