题目内容
3.过曲线S:y=3x-x3上一点A(2,-2)的切线方程为( )| A. | y=-2 | B. | 9x+y-16=0 | C. | 9x+y-16=0或y=-2 | D. | 9x-y-16=0 |
分析 先求出函数的导数,得到函数的大致图象,通过讨论A是切点和A不是切点,从而求出切线的方程.
解答 解:∵y′=3-3x2,
令y′>0,解得:-1<x<1,令y′<0,解得:x>1或x<-1,
∴函数在(-∞,-1)递减,在(-1,1)递增,在(1,+∞)递减,
∴y极小值=-2,y极大值=2,
函数的图象如图所示: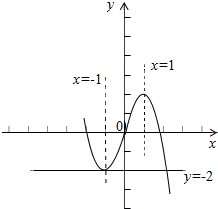 ,
,
①若A不是切点,
∴y=-2是过A(2,-2)的一条切线方程,
②若A是切点,
∵在A点处的切线的斜率是:3-3×4=-9,
∴切线方程是:y+2=-9(x-2),
即:9x+y-16=0,
综上,切线方程是:y=-2或9x+y-16=0,
故选:C.
点评 本题考查了曲线的切线方程,考查导数的应用,本题是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线与椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1在第一、四象限交于A,B两点,若椭圆的左焦点为F,当△AFB的周长最大时,求双曲线的离心率( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | $\frac{9}{4}$ |
18.已知回归直线斜率的估计值为2.1,样本点的中心为(3,4),则回归直线方程为( )
| A. | $\widehat{y}$=2.1x-5.4 | B. | $\widehat{y}$=2.1x-2.3 | C. | $\widehat{y}$=2.1x+2.3 | D. | $\widehat{y}$=2.3x-2.1 |
8.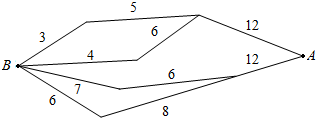 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
13.圆(x-1)2+(y+3)2=2的圆心和半径分别为( )
| A. | (1,-3),$\sqrt{2}$ | B. | (-1,3),2 | C. | (1,3),2 | D. | (-1,3),$\sqrt{2}$ |