题目内容
在△ABC中,设角A,B,C的对边分别为a,b,c,若a=(cosC,2a-c),b=(b,-cosB)且a⊥b,则B= .
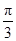
由a⊥b,得a·b=bcosC-(2a-c)cosB=0,
利用正弦定理,可得
sinBcosC-(2sinA-sinC)cosB=sinBcosC+cosBsinC-2sinAcosB=0,即sin(B+C)=sinA=2sinAcosB,
因为sinA≠0,故cosB=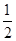 ,
,
又0<B<π,因此B=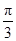 .
.
利用正弦定理,可得
sinBcosC-(2sinA-sinC)cosB=sinBcosC+cosBsinC-2sinAcosB=0,即sin(B+C)=sinA=2sinAcosB,
因为sinA≠0,故cosB=
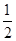 ,
,又0<B<π,因此B=
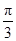 .
.
练习册系列答案
相关题目
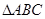 中,
中,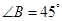 ,
,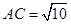 ,
,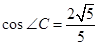 点
点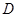 是
是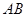 的中点, 求
的中点, 求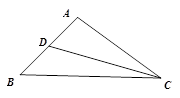
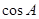 的值和中线
的值和中线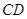 的长
的长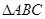 中,
中,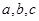 分别是角
分别是角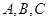 的对边.已知
的对边.已知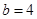 ,
,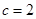 ,
,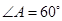 ,则
,则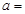 ;
;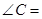 .
.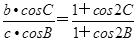 ,试判断△ABC的形状.
,试判断△ABC的形状. 的三内角
的三内角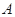 、
、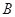 、
、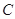 所对边的边长分别为
所对边的边长分别为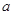 、
、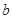 、
、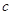 ,且
,且 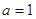 ,
,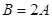 ,则
,则
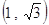
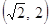
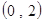
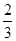 .
.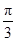 )的值.
)的值.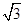 ,则c等于( )
,则c等于( )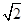 (D)1
(D)1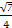 (其中C为锐角).
(其中C为锐角).