Question

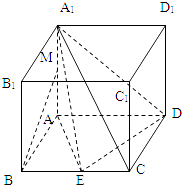
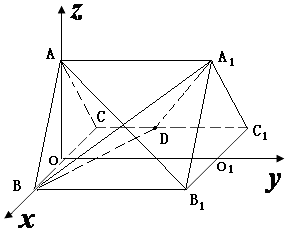
【题目】如图，正三棱柱ABC﹣A1B1C1的所有棱长都为2，D为CC1中点．试用空间向量知识解下列问题：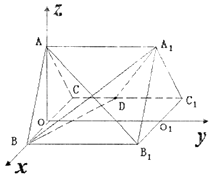

（1）求证：平面ABB1A1⊥平面A1BD；
（2）求二面角A﹣A1D﹣B的大小．

Answer 1

【答案】
（1）证明：取BC中点O，连AO，∵△ABC为正三角形，

∴AO⊥BC，

∵在正三棱柱ABC﹣A1B1C1中，

平面ABC⊥平面BCC1B1，

∴AD⊥平面BCC1B1，

取B1C1中点为O1，以O为原点，

， ， 的方向为x，y，z轴的正方向，

建立空间直角坐标系，

则 ．

∴ ，

∵ ， ．

∴ ， ，∴AB1⊥面A1BD．…（5分）

AA1面A1BD

所以 平面ABB1A1⊥面A1BD

（2）解：设平面A1AD的法向量为 ， ．

，∴ ，∴ ，

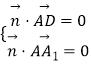令z=1，得 为平面A1AD的一个法向量，

由（1）知AB1⊥面A1BD，

∴ 为平面A1AD的法向量， ，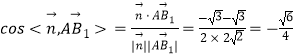

∴二面角A﹣A1D﹣B的正弦值为 = ．

【解析】（1）取BC中点O，连AO，利用正三角形三线合一，及面面垂直的性质可得AO⊥平面BCB1C1 ， 取B1C1中点为O1 ， 以O为原点， ， ， 的方向为x，y，z轴的正方向，建立空间直角坐标系，求出AB1的方向向量，利用向量垂直的充要条件及线面垂直的判定定理可得AB1⊥平面A1BD，即可证明平面ABB1A1⊥平面A1BD；（2）分别求出平面A1AD的法向量和平面A1AD的一个法向量代入向量夹角公式，可得二面角A﹣A1D﹣B的余弦值大小．
【考点精析】通过灵活运用平面与平面垂直的判定，掌握一个平面过另一个平面的垂线，则这两个平面垂直即可以解答此题．