题目内容
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的最大值和最小值;
(2)当a∈R时,求函数f(x)的最小值.
【答案】
(1)解:当a=﹣1时,函数f(x)=x2﹣2x+2的图象是开口朝上,且以直线x=1为对称轴的抛物线,
由x∈[﹣5,5]得:
x=﹣5时,函数取最大值37,
x=1时,函数取最小值1
(2)解:函数f(x)=x2+2ax+2的图象是开口朝上,且以直线x=﹣a为对称轴的抛物线,
若﹣a<﹣5,即a>5,函数f(x)在[﹣5,5]上为增函数,
当x=﹣5时,函数取最小值27﹣10a;
若﹣5≤﹣a≤5,即﹣5≤a≤5,函数f(x)在[﹣5,﹣a]上为减函数,在[﹣a,5]上为增函数,
当x=﹣a时,函数取最小值2﹣a2;
若﹣a>5,即a<﹣5,函数f(x)在[﹣5,5]上为减函数,
当x=5时,函数取最小值27+10a.
综上可得:函数f(x)的最小值为: 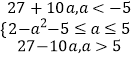
【解析】(1)当a=﹣1时,函数f(x)=x2﹣2x+2的图象是开口朝上,且以直线x=1为对称轴的抛物线,进而可得函数f(x)的最大值和最小值;(2)函数f(x)=x2+2ax+2的图象是开口朝上,且以直线x=﹣a为对称轴的抛物线,分类讨论对称轴与给定区间的位置关系,综合讨论结果,可得答案.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.

练习册系列答案
相关题目