题目内容
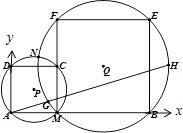
【题目】如图，已知线段AB长度为a（a为定值），在其上任意选取一点M，在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF，⊙P和⊙Q是这两个正方形的外接圆，它们交于点M、N．试以A为坐标原点，建立适当的平面直角坐标系． 
（1）证明：不论点M如何选取，直线MN都通过一定点S；
（2）当 
时，过A作⊙Q的割线，交⊙Q于G、H两点，在线段GH上取一点K，使 
= 
求点K的轨迹．
【答案】
（1）证明：以A为坐标原点，AB为x轴正方向，建立平面直角坐标系．
设M（m，0），则：A（0，0），B（a，0），C（m，m），F（m，a﹣m），
， 
，
⊙P方程为： 
，即：x2+y2﹣mx﹣my=0 ①，
⊙Q方程为： 
即：x2+y2﹣（a+m）x﹣（a﹣m）y+am=0 ②．
①﹣②得，公共弦MN所在直线方程：ax+（a﹣2m）y﹣am=0．
整理得：（ax+ay）+m（﹣2y﹣a）=0，
∴MN恒过定点 
；
（2）解：当 
时， 
，
⊙Q： 
，即： 
．
设G（x1，y1），H（x2，y2），K（x，y），GH所在直线斜率为k，
则： 
， 
， 
，
由题意， 
，即： 
．
把y=kx代入⊙Q方程，得： 
，
由韦达定理得： 
， 
，
∴ 
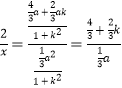，将 
代入整理，得：2x+y﹣a=0．
∴点K的轨迹是直线2x+y﹣a=0被⊙Q所截的一条线段．
【解析】（1）以A为坐标原点，AB为x轴正方向，建立平面直角坐标系，求出圆P、圆Q的方程，由圆系方程求得MN所在直线方程，再由直线系方程可得直线MN都通过一定点；（2）由题意求出M的坐标，得到圆Q的方程，设G（x1 ， y1），H（x2 ， y2），K（x，y），GH所在直线斜率为k，由 
= 
，可得 ，整理后代入根与系数的关系可得点K的轨迹是直线2x+y﹣a=0被⊙Q所截的一条线段．
