题目内容
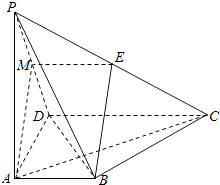
【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点． 
（1）证明：BE∥平面ADP；
（2）求直线BE与平面PDB所成角的正弦值．
【答案】
（1）证明：如图，取PD中点M，连接EM，AM．
∵E，M分别为PC，PD的中点，∴EM∥DC，且EM= 
DC，
又由已知，可得EM∥AB，且EM=AB，
∴四边形ABEM为平行四边形，∴BE∥AM．
∵AM平面PAD，BE平面PAD，
∴BE∥平面ADP．
（2）解：连接BM，由（1）有CD⊥平面PAD，得CD⊥PD，
而EM∥CD，∴PD⊥EM．
又∵AD=AP，M为PD的中点，∴PD⊥AM，
∴PD⊥BE，∴PD⊥平面BEM，
∴平面BEM⊥平面PBD．
∴直线BE在平面PBD内的射影为直线BM，
∵BE⊥EM，∴∠EBM为锐角，
∴∠EBM为直线BE与平面PBD所成的角．
依题意，有PD=2 
，而M为PD中点，
∴AM= ，进而BE= ．
∴在直角三角形BEM中，sin∠EBM= 
= 
= 
．
∴直线BE与平面PDB所成角的正弦值为 ．
【解析】（1）取PD中点M，连接EM，AM，推导出四边形ABEM为平行四边形，由此能证明BE∥平面ADP．（2）连接BM，推导出PD⊥EM，PD⊥AM，从而直线BE在平面PBD内的射影为直线BM，∠EBM为直线BE与平面PBD所成的角，由此能求出直线BE与平面PDB所成角的正弦值．
练习册系列答案
相关题目
