题目内容
【题目】直线x＋y－1＝0被圆(x＋1)2＋y2＝3截得的弦长等于( )
A. 
B. 2
C. 2
D. 4
【答案】B
【解析】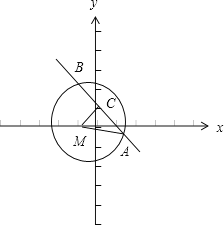
如图,圆(x＋1)2＋y2＝3的圆心为M(1,0)，
圆半径|AM|=
，
圆心M (1,0)到直线x+y1=0的距离：
| 
，
∴直线x+y1=0被圆(x+1)2+y2=3截得的弦长：
.
故选B.
点睛: 本题考查圆的标准方程以及直线和圆的位置关系.判断直线与圆的位置关系一般有两种方法： 1．代数法：将直线方程与圆方程联立方程组，再将二元方 程组转化为一元二次方程，该方程解的情况即对应直 线与圆的位置关系．这种方法具有一般性，适合于判 断直线与圆锥曲线的位置关系，但是计算量较大． 2．几何法：圆心到直线的距离与圆半径比较大小，即可判断直线与圆的位置关系．这种方法的特点是计算量较小．当直线与圆相交时,可利用垂径定理得出圆心到直线的距离,弦长和半径的勾股关系.
练习册系列答案
相关题目
