��Ŀ����
����Ŀ����֪����{an}�ĸ����Ϊ��������ǰn��ĺ�ΪSn �� �Ҷ������m��n��N*��
����Sm+n+S1��2=4a2ma2n ��
��1���� ![]() ��ֵ��
��ֵ��
��2����֤��{an}Ϊ�ȱ����У�
��3����֪����{cn}��{dn}����|cn|=|dn|=an �� p��p��3���Ǹ�����������������{cn}��{dn}��ǰp��ĺͷֱ�ΪTp �� Rp �� ��Tp=Rp �� ��֤��������������k��1��k��p����ck=dk ��
���𰸡�
��1���⣺�ɣ�Sm+n+S1��2=4a2ma2n��ȡm=n=1���ɵ� ![]() ��
��
��a1��a2��0����a2+2a1=2a2����Ϊ ![]() =2
=2
��2��֤�����ɣ�Sm+n+S1��2=4a2ma2n��
��m=n���ɵ�S2n+a1=2a2n����
��S2n+2+a1=2a2n+2����
��m=n+1���ɵ� ![]() ����
����
��۩��ٿɵã�a2n+1=2 ![]() ��2a2n=
��2a2n= ![]()
![]() ����
����
�ک��ۿɵã�a2n+2= ![]() ����
����
�ɢܢݿɵã� ![]() ����
����
�Ѣ���ܿɵã�a2n+1=2a2n��
�Ѣ���ݿɵã�a2n+2=2a2n+1��
�� ![]() =2����
=2���� ![]() =2����
=2���� ![]() ��n��N*��
��n��N*��
��{an}Ϊ�ȱ����У�����Ϊa1������Ϊ2
��3��֤�����ɣ�2����֪��an= ![]() ��
��
��|cn|=|dn|=an= ![]() ��
��
��cp=��dp����cp=��dp��
������cp��0��cp��0��
��Tp�� ![]() ��
�� ![]() =
= ![]() ��
�� ![]() =a1��0��
=a1��0��
Rp�ܩ� ![]() +
+ ![]() =��
=�� ![]() +
+ ![]() =��a1��0��
=��a1��0��
����Tp=Rpì�ܣ���cp=dp��
����Tp��1=Rp��1���ɵ�cp��1=dp��1������cp��2=dp��2������c1=d1��
�������������k��1��k��p����ck=dk��
����������1���ɣ�Sm+n+S1��2=4a2ma2n �� ȡm=n=1���ɵ� ![]() ������a1 �� a2��0�����ɵó�����2���ɣ�Sm+n+S1��2=4a2ma2n �� ��m=n���ɵ�S2n+a1=2a2n �� S2n+2+a1=2a2n+2 �� ��m=n+1���ɵ�
������a1 �� a2��0�����ɵó�����2���ɣ�Sm+n+S1��2=4a2ma2n �� ��m=n���ɵ�S2n+a1=2a2n �� S2n+2+a1=2a2n+2 �� ��m=n+1���ɵ� ![]() �����������ɵã�a2n+1=2a2n �� a2n+2=2a2n+1 �� ���õȱ����е�ͨ�ʽ���ɵó�����3���ɣ�2����֪��an=
�����������ɵã�a2n+1=2a2n �� a2n+2=2a2n+1 �� ���õȱ����е�ͨ�ʽ���ɵó�����3���ɣ�2����֪��an= ![]() ������|cn|=|dn|=an=
������|cn|=|dn|=an= ![]() ���ɵ�cp=��dp �� ��cp=��dp �� ������cp��0��cp��0����Tp��a1��0��Rp�ܩ�a1��0������Tp=Rpì�ܣ��ɵ�cp=dp �� ����Tp��1=Rp��1 �� ����֤����
���ɵ�cp=��dp �� ��cp=��dp �� ������cp��0��cp��0����Tp��a1��0��Rp�ܩ�a1��0������Tp=Rpì�ܣ��ɵ�cp=dp �� ����Tp��1=Rp��1 �� ����֤����
�����㾫����ͨ������������е�ǰn��ͺ����е�ͨ�ʽ����������{an}��ǰn���sn��ͨ��an�Ĺ�ϵ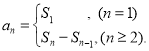 ���������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ�����Խ����⣮
���������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ�����Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij��ѧ������ij��ȫ��45��ͬѧ�μ��鷨���ź��ݽ����ŵ�������������±�������λ���ˣ�
�μ��鷨���� | δ�μ��鷨���� | |
�μ��ݽ����� | 8 | 5 |
δ�μ��ݽ����� | 2 | 30 |
��1���Ӹð����ѡ1��ͬѧ�����ͬѧ���ٲμ�һ�����ŵĸ��ʣ�
��2���ڼȲμ��鷨�����ֲμ��ݽ����ŵ�8��ͬѧ�У���5����ͬѧA1 �� A2 �� A3 �� A4 �� A5 �� 3��ŮͬѧB1 �� B2 �� B3 �� �ִ���5����ͬѧ��3��Ůͬѧ�и����ѡ1�ˣ���A1��ѡ����B1δ��ѡ�еĸ��ʣ�
