Question

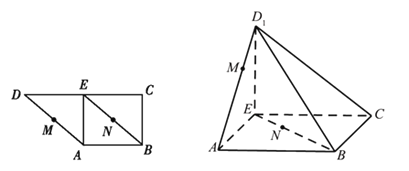
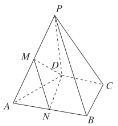
【题目】如图，已知在四棱锥中，底面为矩形，侧面底面，，.

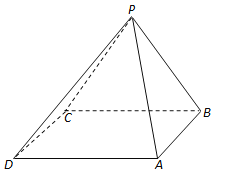
（1）求二面角的大小；

（2）求点到平面的距离.

Answer 1

【答案】（1）（2）

【解析】

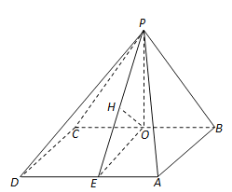
（1）在平面PBC内作PO⊥BC，O为垂足，在底面ABCD内作OE⊥BC，OE∩AD＝E，连结PE，由已知ABCD为矩形，推导出PO⊥底面ABCD，PO⊥AD，OE⊥BC，从而OE⊥AD，AD⊥平面POE，AD⊥PE，再由AD⊥OE，得∠OEP是二面角PADB的平面角．由此能求出二面角PADB的大小；

（2）推导出BC∥平面PAD，从而点B到平面PAD的距离等于点O到平面PA的距离．在Rt△POE中作OH⊥PE，H为垂足，推导出OH⊥平面PAD，从而点O到平面PAD的距离即为OH的长，此能求出点B到平面PAD的距离．

解：（1）在平面内作，为垂足，

在中，，所以.

在底面内作，，连结，

由已知为矩形，易知也是矩形，故.

又平面底面，平面底面，

平面，所以底面，

而底面，所以，

又，，所以，

而平面，平面，

，所以平面，

因为平面，所以，

又因为，所以是二面角的平面角.

因为底面，底面，所以，

在中，，

所以，故二面角的大小为.

（2）因为，而平面，平面，

所以平面，又，，

所以，点到平面的距离等于点到平面的距离.

在中作，为垂足，

由（1）知平面，而平面，所以，

又，平面，平面，所以平面，

所以，点到平面的距离即为的长.

在中，，

即，

综上，点到平面的距离为.