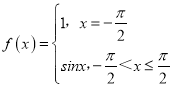Question

【题目】已知AOB的一个顶点O是抛物线C：的顶点，A、B两点都在C上，且=0，

（1）证明：直线AB恒过定点P（2，0）

（2）求AOB面积的最小值

Answer 1

【答案】（1）证明过程见详解；（2）4.

【解析】

（1）由得所在直线与所在的直线垂直，设出直线方程，与抛物线方程联立求出、两点的坐标，由两点式得直线AB的方程，化简整理即可得到答案.

（2）由（1）的结论设出直线AB的方程，联立直线与抛物线的方程化简，由根与系数的关系及弦长公式即可求得的面积的表达式，利用二次函数的性质即可得到答案.

（1）依题设所在的直线为，

因为，所以，

所以所在的直线为,

由 解得或，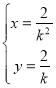

所以点的坐标为.

同理由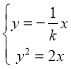可得点的坐标为

所以所在的直线方程为，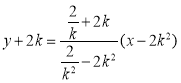

化简整理得：，

所以对任何不为0的实数，当时，恒有，

所以直线AB恒过定点.

（2）由（1）知直线AB恒过定点，

则可直线AB的方程为，设

由得,

则

所以

，

所以

所以当时，的面积取得最小值为