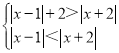题目内容
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1,x2,当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1,y2,使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.则①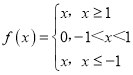 ,②
,②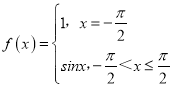 ,③
,③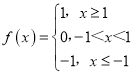 ,④
,④![]() ,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
【答案】①③ 9
【解析】
①③两个函数满足题意,②是严格单调递增的函数,不合题意,④当x1![]() ,x2∈(1,
,x2∈(1,![]() ),f(x1)>f(x2),不合题意;分别列举出满足条件的函数关系即可得解.
),f(x1)>f(x2),不合题意;分别列举出满足条件的函数关系即可得解.
由已知中:函数f(x)定义域内任意的两个自变量的值x1,x2,
当x1<x2时,都有f(x1)≤f(x2),
且存在两个不相等的自变量值y1,y2,使得f(y1)=f(y2),
就称f(x)为定义域上的不严格的增函数.
①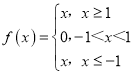 ,满足条件,为定义在R上的不严格的增函数;
,满足条件,为定义在R上的不严格的增函数;
②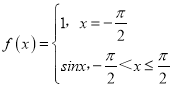 ,当x1
,当x1![]() ,x2∈(
,x2∈(![]() ,
,![]() ),f(x1)>f(x2),故不是不严格的增函数;
),f(x1)>f(x2),故不是不严格的增函数;
③ ,满足条件,为定义在R上的不严格的增函数;
,满足条件,为定义在R上的不严格的增函数;
④![]() ,当x1
,当x1![]() ,x2∈(1,
,x2∈(1,![]() ),f(x1)>f(x2),故不是不严格的增函数;
),f(x1)>f(x2),故不是不严格的增函数;
故已知的四个函数中为不严格增函数的是①③;
∵函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,
则满足条件的函数g(x)有:
g(1)=g(2)=g(3)=1,
g(1)=g(2)=g(3)=2,
g(1)=g(2)=g(3)=3,
g(1)=g(2)=1,g(3)=2,
g(1)=g(2)=1,g(3)=3,
g(1)=g(2)=2,g(3)=3,
g(1)=1,g(2)=g(3)=2,
g(1)=1,g(2)=g(3)=3,
g(1)=2,g(2)=g(3)=3,
故这样的函数共有9个,
故答案为:①③;9.