题目内容
如图所示,已知抛物线方程为y2=4x,其焦点为F,准线为l,A点为抛物线上异于顶点的一个动点,射线HAE垂直于准线l,垂足为H,C点在x轴正半轴上,且四边形AHFC是平行四边形,线段AF和AC的延长线分别交抛物线于点B和点D.

(1)证明:∠BAD=∠EAD;
(2)求△ABD面积的最小值,并写出此时A点的坐标.

(1)证明:∠BAD=∠EAD;
(2)求△ABD面积的最小值,并写出此时A点的坐标.
(1)见解析(2)16 ,(1,±2)
(1)证明:由抛物线定义得|AH|=|AF|,∴∠AHF=∠AFH.
又∵四边形AHFC是平行四边形,∴HF∥AC,∴∠AHF=∠EAD,∠AFH=∠BAD.
综上可得∠BAD=∠EAD.
(2)易知焦点F(1,0),准线l方程为x=-1,设A点坐标为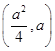 (a≠0),
(a≠0),
则直线AB方程为4ax-(a2-4)y-4a=0(包括AB⊥x轴的情况),
结合y2=4x得4a2x2-(a4+16)x+4a2=0,
根据抛物线定义,可知|AB|=xA+xB+2=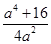 +2=
+2=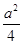 +
+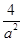 +2≥4(当且仅当a=±2时等号成立).
+2≥4(当且仅当a=±2时等号成立).
另外,结合kAD=kHF=-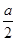 ,可得直线AD方程为y=-
,可得直线AD方程为y=-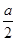 x+
x+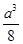 +a,
+a,
结合y2=4x得ay2+8y-a3-8a=0,由于yD+yA=-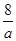 ,
,
∴yD=-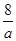 -a.又∵∠BAD=∠EAD,
-a.又∵∠BAD=∠EAD,
∴D点到直线AB的距离即为D点到直线AE的距离,即d=|yD-yA|=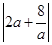 ≥8(当且仅当a=±2时等号成立).
≥8(当且仅当a=±2时等号成立).
∴S△ABD=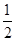 ·|AB|·d≥
·|AB|·d≥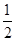 ×4×8=16(当且仅当a=±2时取“=”号).
×4×8=16(当且仅当a=±2时取“=”号).
此时A点坐标为(1,±2).
又∵四边形AHFC是平行四边形,∴HF∥AC,∴∠AHF=∠EAD,∠AFH=∠BAD.
综上可得∠BAD=∠EAD.
(2)易知焦点F(1,0),准线l方程为x=-1,设A点坐标为
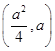 (a≠0),
(a≠0),则直线AB方程为4ax-(a2-4)y-4a=0(包括AB⊥x轴的情况),
结合y2=4x得4a2x2-(a4+16)x+4a2=0,
根据抛物线定义,可知|AB|=xA+xB+2=
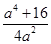 +2=
+2=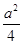 +
+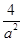 +2≥4(当且仅当a=±2时等号成立).
+2≥4(当且仅当a=±2时等号成立).另外,结合kAD=kHF=-
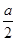 ,可得直线AD方程为y=-
,可得直线AD方程为y=-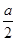 x+
x+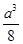 +a,
+a,结合y2=4x得ay2+8y-a3-8a=0,由于yD+yA=-
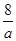 ,
,∴yD=-
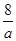 -a.又∵∠BAD=∠EAD,
-a.又∵∠BAD=∠EAD,∴D点到直线AB的距离即为D点到直线AE的距离,即d=|yD-yA|=
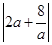 ≥8(当且仅当a=±2时等号成立).
≥8(当且仅当a=±2时等号成立).∴S△ABD=
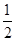 ·|AB|·d≥
·|AB|·d≥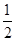 ×4×8=16(当且仅当a=±2时取“=”号).
×4×8=16(当且仅当a=±2时取“=”号).此时A点坐标为(1,±2).

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
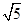 ,则抛物线的方程为( )
,则抛物线的方程为( ) ),C(x,y),若
),C(x,y),若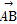 ⊥
⊥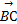 ,则动点C的轨迹方程是_________.
,则动点C的轨迹方程是_________.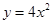 上的一点
上的一点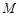 到焦点的距离为1,则点
到焦点的距离为1,则点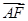 =
=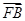 ,
,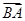 ·
·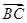 =36,则抛物线的方程为________.
=36,则抛物线的方程为________.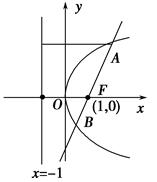
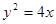 的焦点
的焦点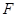 ,该抛物线上的一点
,该抛物线上的一点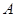 到
到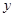 轴的距离为3,则
轴的距离为3,则