题目内容
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
(1)y2=8x.(2)24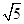
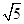
(1)易知直线与抛物线的交点坐标为(8,-8),∴82=2p×8,∴2p=8,∴抛物线方程为y2=8x.
(2)直线l2与l1垂直,
故可设l2:x=y+m,A(x1,y1),B(x2,y2),且直线l2与x轴的交点为M.
由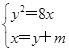 得y2-8y-8m=0,Δ=64+32m>0,∴m>-2.
得y2-8y-8m=0,Δ=64+32m>0,∴m>-2.
y1+y2=8,y1y2=-8m,∴x1x2= =m2.
=m2.
由题意可知OA⊥OB,即x1x2+y1y2=m2-8m=0,∴m=8或m=0(舍),
∴l2:x=y+8,M(8,0),
故S△FAB=S△FMB+S△FMA= |FM|·|y1-y2|=3
|FM|·|y1-y2|=3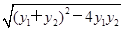 =24
=24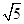 .?
.?
(2)直线l2与l1垂直,
故可设l2:x=y+m,A(x1,y1),B(x2,y2),且直线l2与x轴的交点为M.
由
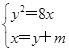 得y2-8y-8m=0,Δ=64+32m>0,∴m>-2.
得y2-8y-8m=0,Δ=64+32m>0,∴m>-2.y1+y2=8,y1y2=-8m,∴x1x2=
 =m2.
=m2.由题意可知OA⊥OB,即x1x2+y1y2=m2-8m=0,∴m=8或m=0(舍),
∴l2:x=y+8,M(8,0),
故S△FAB=S△FMB+S△FMA=
 |FM|·|y1-y2|=3
|FM|·|y1-y2|=3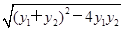 =24
=24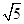 .?
.?
练习册系列答案
相关题目
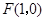 ,直线
,直线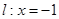 ,
,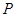 为平面上的动点,过点
为平面上的动点,过点 的垂线,垂足为点
的垂线,垂足为点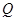 ,且
,且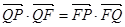 .
. 的方程;
的方程;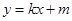 与曲线
与曲线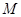 ,且与直线
,且与直线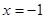 相交于点
相交于点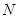 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点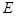 ,使得以
,使得以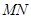 为直径的圆恒过此定点
为直径的圆恒过此定点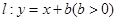 ,抛物线
,抛物线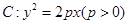 ,已知点
,已知点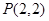 在抛物线
在抛物线 上,且抛物线
上,且抛物线 的距离的最小值为
的距离的最小值为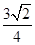 .
.
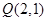 的任一直线(不经过点
的任一直线(不经过点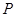 )与抛物线
)与抛物线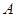 、
、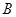 两点,直线
两点,直线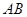 与直线
与直线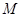 ,记直线
,记直线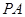 ,
,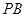 ,
,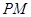 的斜率分别为
的斜率分别为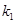 ,
,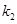 ,
, 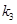 .问:是否存在实数
.问:是否存在实数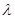 ,使得
,使得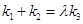 ?若存在,试求出
?若存在,试求出
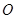 ,焦点
,焦点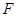 在
在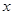 轴上,抛物线上的点
轴上,抛物线上的点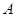 到
到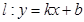 与抛物线交于
与抛物线交于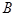 ,
,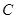 两点.
两点.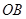 ,
,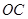 的倾斜角之和为
的倾斜角之和为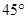 时,证明直线
时,证明直线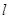 过定点.
过定点. x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4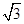
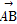 ·
·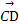 的值是 .
的值是 .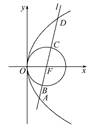
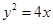 焦点
焦点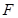 的直线交其于
的直线交其于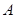 ,
,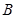 两点,
两点,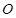 为坐标原点.若
为坐标原点.若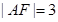 ,则
,则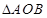 的面积为( )
的面积为( )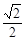
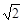
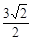
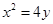 ,下列描述正确的是
,下列描述正确的是