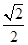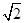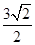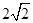题目内容
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点.若|AF|=3,
则|BF|=________.
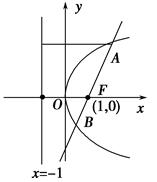
则|BF|=________.


设∠AFx=θ(0<θ<π),|BF|=m,则xA=1+3cos θ,
xB=1+mcos(π-θ)=1-mcos θ.又y2=4x的准线l为x=-1,
∴|AF|=1+xA=2+3cos θ,因此3=2+3cos θ,∴cos θ= .
.
∴m=1+xB,则m=2-mcos θ,所以|BF|=m= =
= .
.
xB=1+mcos(π-θ)=1-mcos θ.又y2=4x的准线l为x=-1,
∴|AF|=1+xA=2+3cos θ,因此3=2+3cos θ,∴cos θ=
 .
.∴m=1+xB,则m=2-mcos θ,所以|BF|=m=
 =
= .
.
练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目

 ,焦点
,焦点 在
在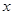 轴上,抛物线上的点
轴上,抛物线上的点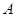 到
到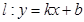 与抛物线交于
与抛物线交于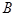 ,
,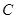 两点.
两点.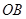 ,
,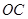 的倾斜角之和为
的倾斜角之和为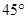 时,证明直线
时,证明直线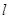 过定点.
过定点. x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4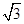
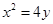 ,下列描述正确的是
,下列描述正确的是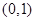
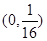
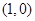
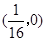
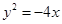 上一点
上一点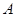 到焦点的距离等于5,则
到焦点的距离等于5,则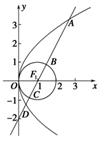
 为坐标原点,
为坐标原点,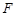 为抛物线
为抛物线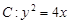 的焦点,
的焦点,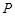 为抛物线
为抛物线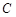 上一点,若
上一点,若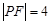 ,则
,则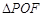 的面积为 .
的面积为 .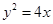 的焦点
的焦点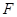 的直线交抛物线于
的直线交抛物线于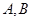 两点,点
两点,点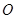 是原点,若
是原点,若 ;则
;则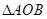 的面积为 ( )
的面积为 ( )