题目内容
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方程为( )
| A.y2=4x或y2=8x | B.y2=2x或y2=8x |
| C.y2=4x或y2=16x | D.y2=2x或y2=16x |
C
由已知得抛物线的焦点F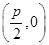 ,设点A(0,2),抛物线上点M(x0,y0),则
,设点A(0,2),抛物线上点M(x0,y0),则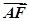 =
=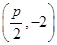 ,
,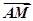 =
=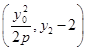 .由已知得,
.由已知得, ·
· =0,
=0,
即y02-8y0+16=0,因而y0=4,M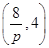 .
.
由|MF|=5得,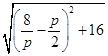 =5,
=5,
又p>0,解得p=2或p=8.
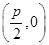 ,设点A(0,2),抛物线上点M(x0,y0),则
,设点A(0,2),抛物线上点M(x0,y0),则 =
=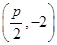 ,
,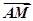 =
=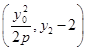 .由已知得,
.由已知得,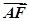 ·
·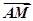 =0,
=0,即y02-8y0+16=0,因而y0=4,M
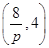 .
.由|MF|=5得,
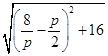 =5,
=5,又p>0,解得p=2或p=8.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目

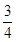

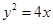 焦点
焦点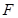 的直线交其于
的直线交其于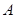 ,
,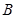 两点,
两点,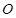 为坐标原点.若
为坐标原点.若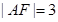 ,则
,则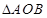 的面积为( )
的面积为( )
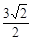
 的焦点坐标为
的焦点坐标为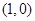 ,则准线方程为 .
,则准线方程为 .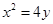 ,下列描述正确的是
,下列描述正确的是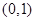
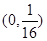
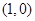
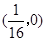
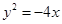 上一点
上一点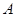 到焦点的距离等于5,则
到焦点的距离等于5,则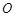 为坐标原点,
为坐标原点,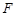 为抛物线
为抛物线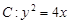 的焦点,
的焦点,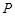 为抛物线
为抛物线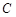 上一点,若
上一点,若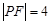 ,则
,则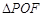 的面积为 .
的面积为 .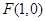 是抛物线
是抛物线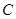 :
: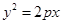 的焦点,则
的焦点,则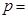 _______.
_______.