题目内容
【题目】在一次数学测验后,数学老师将某班全体学生(50人)的数学成绩进行初步统计后交给其班主任(如表).
分数 | 5060 | 60~70 | 70-80 | 80-90 | 90~100 |
人数 | 2 | 6 | 10 | 20 | 12 |
请你帮助这位班主任完成下面的统计分析工作:
(1)列出频率分布表;
(2)画出频率分布直方图及频率折线图;
(3)从频率分布直方图估计出该班同学成绩的众数、中位数和平均数.
【答案】(1)见解析;(2)见解析;(3)85,83.5,81.8.
【解析】
(1)根据表中数据得到频数,并计算出对应频率,从而得到频率分布表;
(2)根据频率计算可得每个小矩形对应的高,从而得到频率分布直方图;将每个小矩形上端横坐标中点连线即可得到频率折线图;
(3)根据频率分布直方图中众数、中位数和平均数的估计方法计算可得结果.
(1)计算对应的频率,列出频率分布表,如下:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(2)根据频率分布表,画出频率分布直方图及频率折线图,如下:
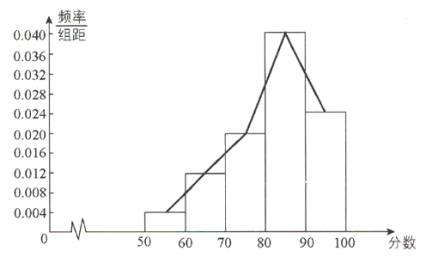
(3)根据频率分布直方图知,最高的一组数据为![]()
![]() 众数为
众数为![]()
又![]() ,
,![]()
![]() 中位数在
中位数在![]() 内,设中位数为
内,设中位数为![]()
则![]() ,解得:
,解得:![]() ,即中位数为
,即中位数为![]()
平均数为:![]()

【题目】交通部门调查在高速公路上的平均车速情况,随机抽查了60名家庭轿车驾驶员,统计其中有40名男性驾驶员,其中平均车速超过![]() 的有30人,不超过
的有30人,不超过![]() 的有10人;在其余20名女性驾驶员中,平均车速超过
的有10人;在其余20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为,家庭轿车平均车速超过
的把握认为,家庭轿车平均车速超过![]() 与驾驶员的性别有关;
与驾驶员的性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
(2)根据这些样本数据来估计总体,随机调查3辆家庭轿车,记这3辆车中,驾驶员为女性且平均车速不超过![]() 的人数为
的人数为![]() ,假定抽取的结果相互独立,求
,假定抽取的结果相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: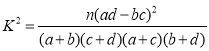
![]()
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
