题目内容
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有三个不同的零点,求
有三个不同的零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)![]() ,对a分类讨论,从而得到
,对a分类讨论,从而得到![]() 的单调性;
的单调性;
(2)![]() ,则
,则![]() ,对a分类讨论,研究函数
,对a分类讨论,研究函数![]() 的图象走势,从而得到
的图象走势,从而得到![]() 的取值范围.
的取值范围.
试题解析:
(1)由已知![]() 的定乂域为
的定乂域为![]() ,又
,又![]() ,
,
当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() 时,令
时,令![]() 得
得![]() ;令
;令![]() 得
得![]() .
.
综上所述,当![]() 时,
时,![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
(2)由题意![]() ,则
,则![]() ,
,
当![]() 时,∵
时,∵![]() ,
,
∴![]() 在
在![]() 上为增函数,不符合题意.
上为增函数,不符合题意.
当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() .
.
令![]() 的两根分别为
的两根分别为![]() 且
且![]() ,
,
则∵![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上为增函数.
上为增函数.
∵![]() ,∴
,∴![]() 在
在![]() 上只有一个零点 1,且
上只有一个零点 1,且![]() 。
。
∴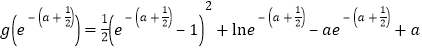
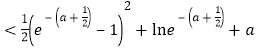 ,
,
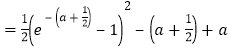 ,
,
![]() .
.
∵![]() ,又当
,又当![]() 时,
时,![]() .∴
.∴![]()
∴![]() 在
在![]() 上必有一个零点.
上必有一个零点.
∴![]()
![]() .
.
∵![]() ,又当
,又当![]() 时,
时,![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上必有一个零点.
上必有一个零点.
综上所述,故![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
【题目】下表为北京市居民用水阶梯水价表(单位:元/立方米).
阶梯 | 户年用水量 (立方米) | 水价 | 其中 | ||
自来水费 | 水资源费 | 污水处理费 | |||
第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
第三阶梯 | 260以上 | 9.00 | 6.07 | ||
(Ⅰ)试写出水费![]() (元)与用水量
(元)与用水量![]() (立方米)之间的函数关系式;
(立方米)之间的函数关系式;
(Ⅱ)若某户居民年交水费1040元,求其中自来水费、水资源费及污水处理费各是多少?