题目内容
12．6个人站成一排，若调换其中三个人的位置，有多少种不同的换法？分析 这是一个分步问题，使用乘法原理：第一步．先从七个人里选三个进行调换，第二步．因为每个人都不能坐在原来的位置上，因此第一个人有两种坐法，被坐了自己椅子的那个人只能坐在第三个人的椅子上（一种坐法），才能保证第三个人也不坐在自己的椅子上．因此三个人调换有两种调换方法．
解答 解：使用乘法原理
第一步．先从6个人里选3个进行调换
第二步．因为每个人都不能坐在原来的位置上，因此第一个人有两种坐法，被坐了自己椅子的那个人只能坐在第三个人的椅子上（一种坐法），才能保证第三个人也不坐在自己的椅子上．因此三个人调换有两种调换方法．
故不同的调换方法有C63×2=40．
点评 本小题主要考查排列、组合及简单计数问题、乘法原理等基础知识，考查分析问题解决问题的能力．属于基础题．
练习册系列答案
相关题目
2．
把一个底面边长和高都为6的正三棱锥（底面是正三角形，从顶点向底面作垂线，垂足是底面的中心的三棱锥）P-ABC的底面ABC放置在平面α上，现让三棱锥绕棱BC逆时针方向旋转，使侧面PBC落在α内，则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是（ ）
把一个底面边长和高都为6的正三棱锥（底面是正三角形，从顶点向底面作垂线，垂足是底面的中心的三棱锥）P-ABC的底面ABC放置在平面α上，现让三棱锥绕棱BC逆时针方向旋转，使侧面PBC落在α内，则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是（ ）| A． | [$\frac{54\sqrt{13}}{13}$，12$\sqrt{3}$] | B． | [$\frac{54\sqrt{13}}{13}$，9$\sqrt{3}$] | C． | [$\frac{48\sqrt{13}}{13}$，12$\sqrt{3}$] | D． | [$\frac{48\sqrt{13}}{13}$，3$\sqrt{39}$] |
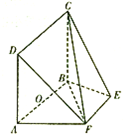如图，等腰梯形ABEF中，AB∥EF，AB=2，AD=AF=1，AF⊥BF，O为AB的中点，矩形ABCD所在平面与平面ABEF互相垂直．
17．执行如图所示的程序框图，如果输入的x∈R，则输出的h（x）的最小值是（ ）
| A． | $\frac{3}{4}$ | B． | 3 | C． | 4 | D． | 7 |