题目内容
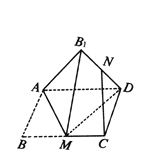
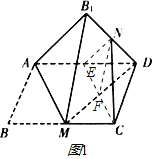
【题目】如图,在矩形ABCD中,M为BC的中点,将△AMB沿直线AM翻折成△AB1M,连接B1D,N为B1D的中点,则在翻折过程中,下列说法正确的是( )
A.存在某个位置,使得CN⊥AB1
B.CN的长是定值
C.若AB=BM,则AM⊥B1D
D.若AB=BM=1,当三棱锥B1-AMD的体积最大时,三棱锥B1-AMD的外接球的表面积是4π
【答案】BD
【解析】
![]() 中,取
中,取![]() 中点
中点![]() ,连接
,连接![]() 交
交![]() 与
与![]() ,由题意判断三线
,由题意判断三线![]() ,
,![]() ,
,![]() 共面共点,得出
共面共点,得出![]() 不成立;
不成立;
![]() 中,利用余弦定理可得
中,利用余弦定理可得![]() 是定值,判断
是定值,判断![]() 正确;
正确;
![]() 中,取
中,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,由题意判断
,由题意判断![]() 不成立;
不成立;
![]() 中,当三棱锥
中,当三棱锥![]() 的体积最大时,求出该三棱锥外接球的表面积即可.
的体积最大时,求出该三棱锥外接球的表面积即可.
解:对于![]() :如图1,取
:如图1,取![]() 中点
中点![]() ,连接
,连接![]() 交
交![]() 与
与![]() ,
,
则![]() ,
,![]() ,
,
如果![]() ,可得到
,可得到![]() ,
,
又![]() ,且三线
,且三线![]() ,
,![]() ,
,![]() 共面共点,不可能,则
共面共点,不可能,则![]() 错误.
错误.
对于![]() :如图1,可得由
:如图1,可得由![]() (定值),
(定值),
![]() (定值),
(定值),![]() (定值),
(定值),
由余弦定理可得![]() ,
,
所以![]() 是定值,则
是定值,则![]() 正确.
正确.
对于![]() :如图2,取
:如图2,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
由题意得![]() 面
面![]() ,即可得
,即可得![]() ,
,
从而![]() ,由题意不成立,可得
,由题意不成立,可得![]() 错误.
错误.
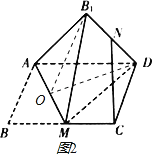
对于![]() :当平面
:当平面![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 的体积最大,
的体积最大,
由题意得![]() 中点
中点![]() 就是三棱锥
就是三棱锥![]() 的外接球的球心,
的外接球的球心,
球半径为1,表面积是![]() ,则
,则![]() 正确.
正确.
故选:BD.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目